给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

说明:

1. 你可以假设矩阵不可变。
2. 会多次调用 sumRegion 方法。
3. 你可以假设 row1 ≤ row2 且 col1 ≤ col2。

Solution

• 直接暴力求解

# @lc code=start
class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            return
        self.row = len(matrix)
        self.col = len(matrix[0])
        self.matrix = matrix

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        res = 0
        for i in range(row1, row2+1):
            for j in range(col1, col2+1):
                res += self.matrix[i][j]
        return res


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)
# @lc code=end

@powcai ——动态规划

• 先求矩阵每个元素的左上方元素之和

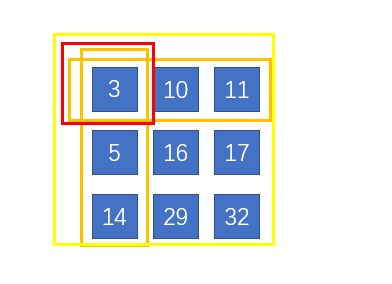
  3 7 1 3 10 11

  2 4 0 –> 5 16 17

  9 4 2 14 29 32

• 然后求 sumRegion

  

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            return
        row = len(matrix)
        col = len(matrix[0])
        self.dp = [[0]*(col+1) for _ in range(row+1)]
        for i in range(1, row+1):
            for j in range(1,col+1):
                self.dp[i][j] = self.dp[i-1][j]+self.dp[i][j-1]+matrix[i-1][j-1]-self.dp[i-1][j-1]
        
    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.dp[row2+1][col2+1]-self.dp[row2+1][col1]-self.dp[row1][col2+1]+self.dp[row1][col1]