本文最后更新于:2022年4月9日 中午
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
Solution
参考 回溯算法解题套路框架 的思路
回溯算法的核心框架
| for 选择 in 选择列表:
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
路径.remove(选择)
将该选择再加入选择列表
|
- 将track加入res要使用深拷贝,不然会出现结果为全空的情况,这是因为append只是映射出一条指向track的链接。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
length = len(nums)
def backtrack(nums, track):
if len(track) == length:
new = copy.deepcopy(track)
res.append(new)
for i in range(len(nums)):
if nums[i] in track:
continue
track.append(nums[i])
backtrack(nums, track)
track.remove(nums[i])
backtrack(nums, [])
return res
|
powcai
| class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
length = len(nums)
def backtrack(nums, track):
if len(track) == length:
res.append(track)
for i in range(len(nums)):
backtrack(nums[:i]+nums[i+1:], track+[nums[i]])
backtrack(nums, [])
return res
|
参考 代码随想录
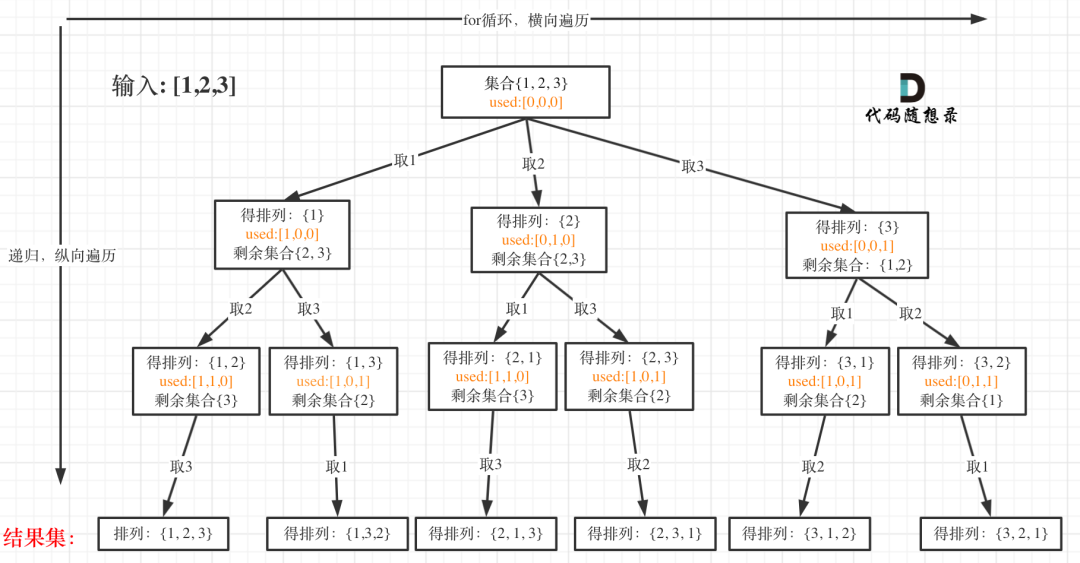
- 处理排列问题不需要使用 index,排列是有顺序的。
- 排列问题需要一个 used数组,标记已经选择的元素,一个排列里一个元素只能使用一次。树枝去重
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Solution {
private:
vector<vector<int>> res;
vector<bool> used;
void dfs(const vector<int>& nums, vector<int>& cur){
if(cur.size()==nums.size()){
res.push_back(cur);
return;
}
for(int i=0; i<nums.size(); ++i){
if(!used[i]){
used[i]=true;
cur.push_back(nums[i]);
dfs(nums, cur);
cur.pop_back();
used[i]=false;
}
}
return;
}
public:
vector<vector<int>> permute(vector<int>& nums) {
res.clear();
if(nums.size()==0)
return res;
used = vector<bool>(nums.size(), false);
vector<int> cur;
dfs(nums, cur);
return res;
}
};
|
注:排列问题
- 每层都是从0开始搜索而不是 startIndex
- 需要 used 数组记录path里都放了哪些元素了
