给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

输入：s = "a", t = "a"
输出："a"

提示：

• 1 <= s.length, t.length <= 105
• s 和 t 由英文字母组成

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？

Solution

• 滑动窗口算法

参考 滑动窗口技巧 的思路

# @lc code=start
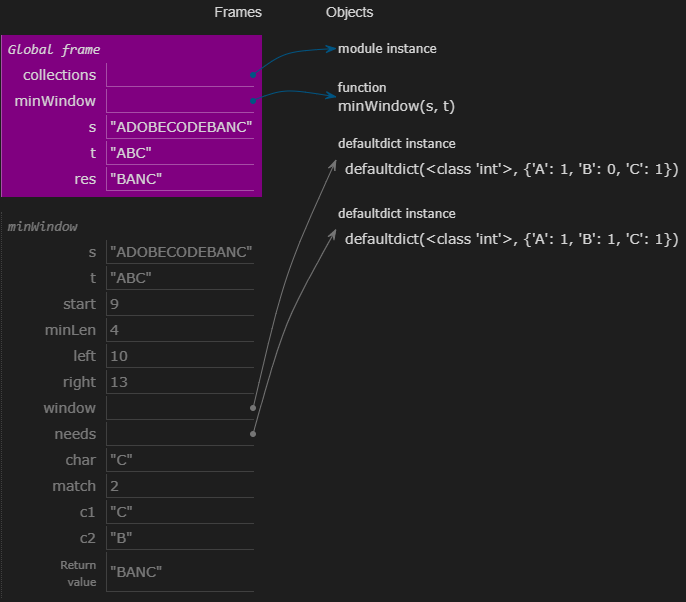
class Solution:
    def minWindow(self, s: str, t: str) -> str:
        start, minLen = 0, float('inf')
        left, right = 0, 0
        
        window = collections.defaultdict(int)
        needs = collections.defaultdict(int)
        for char in t:
            needs[char] += 1

        match = 0
        while(right < len(s)):
            c1 = s[right]
            if c1 in needs:
                window[c1] += 1
                if window[c1] == needs[c1]:
                    match += 1
            right += 1
            
            while match==len(needs):
                if (right-left < minLen):
                    start = left
                    minLen = right -left
                c2 = s[left]
                if c2 in needs:
                    window[c2] -= 1
                    if window[c2] < needs[c2]:
                        match -= 1
                left += 1
        
        return "" if minLen>len(s) else s[start:start+minLen]
        
# @lc code=end

注：滑动窗口算法框架

void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

c++

参考 @mcdull0921 、@汎汎杨舟

class Solution {
public:
    string minWindow(string s, string t) {
        vector<int> needs(128,0);
        int cnt = t.size(); // 需要匹配的大小
        for(char c : t)
            needs[c] ++;
        
        int l=0, r=0, start=0, size=INT_MAX;
        while(r<s.size()){
            char c = s[r];
            if(needs[c]>0)
                cnt--;
            needs[c]--;
            if(cnt==0){
                while(l<r && needs[s[l]]<0){
                    needs[s[l++]] ++;
                }
                if(r-l+1 < size){
                    size = r-l+1;
                    start = l;
                }
                needs[s[l++]]++;
                cnt++;
            }
            r++;
        }
        return size==INT_MAX ? "" : s.substr(start, size);
    }
};