给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3:

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:

• 1 <= text1.length <= 1000
• 1 <= text2.length <= 1000
• 输入的字符串只含有小写英文字符。

Solution

参考：《算法小抄》2.6

其他相同题目：[1035 不相交的线]

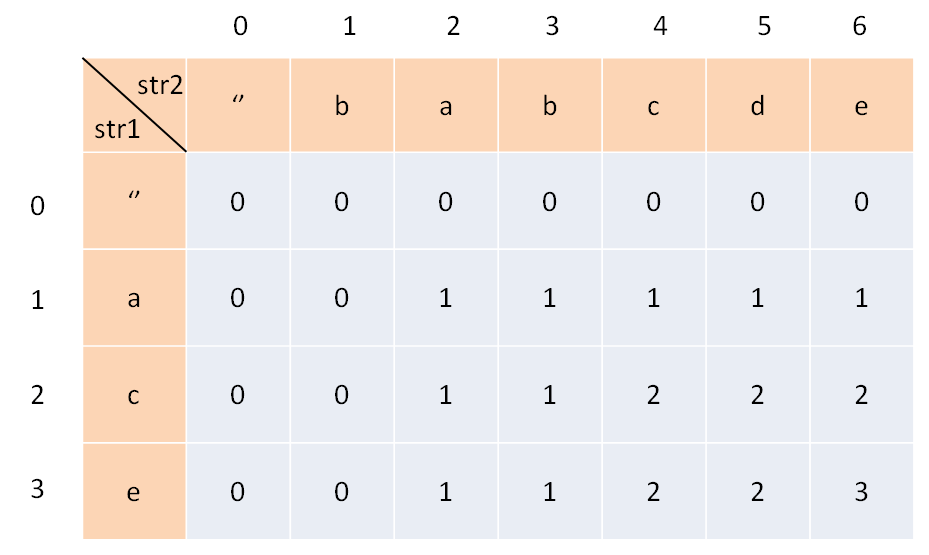
• 动态规划，使用 dp table
• dp[i] [j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i] [j]

# @lc code=start
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        len1=len(text1)
        len2=len(text2)
        if len1*len2 == 0: return 0
        dp=[[0]*(len2+1) for _ in range(len1+1)]
        
        for i in range(1, len1+1):
            for j in range(1, len2+1):
                if text1[i-1]==text2[j-1]:
                    dp[i][j]=1+dp[i-1][j-1]
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])
        return dp[-1][-1]
# @lc code=end

cpp

// @lc code=start
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size();
        int n2 = text2.size();
        if (n1 * n2 == 0) return 0;

        vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));
        for (int i = 1; i <= n1; ++i) {
            for (int j = 1; j <= n2; ++j) {
                if (text1[i-1] == text2[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        return dp[n1][n2];
    }
};
// @lc code=end

输出具体字符串，见 NC127 最长公共子串

class Solution {
public:
    /**
     * longest common substring
     * @param str1 string字符串 the string
     * @param str2 string字符串 the string
     * @return string字符串
     */
    string LCS(string str1, string str2) {
        // write code here
        int n1 = str1.size();
        int n2 = str2.size();
        vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));
        int maxLen = 0, end = 0;

        for (int i = 1; i <= n1; ++i) {
            for (int j = 1; j <= n2; ++j) {
                if (str1[i-1] == str2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = 0;
                if (dp[i][j] > maxLen) {
                    maxLen = dp[i][j];
                    end = j-1;
                }
            }
        }
        string res = "";
        if (maxLen == 0) return "-1";
        else
            res = str2.substr(end - maxLen + 1, maxLen);
        return res;
    }
};