给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

Solution

参考：《算法小抄》2.6、代码随想录

• 递归，开销大，超时
• 框架

if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

code

# @lc code=start
class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        def dp(i, j):
            if i==-1: return j+1
            if j==-1: return i+1
            
            if word1[i]==word2[j]:
                return dp(i-1, j-1)
            else:
                return min(
                    dp(i, j-1)+1, dp(i-1,j)+1, dp(i-1,j-1)+1
                )
        return dp(len(word1)-1, len(word2)-1)
# @lc code=end

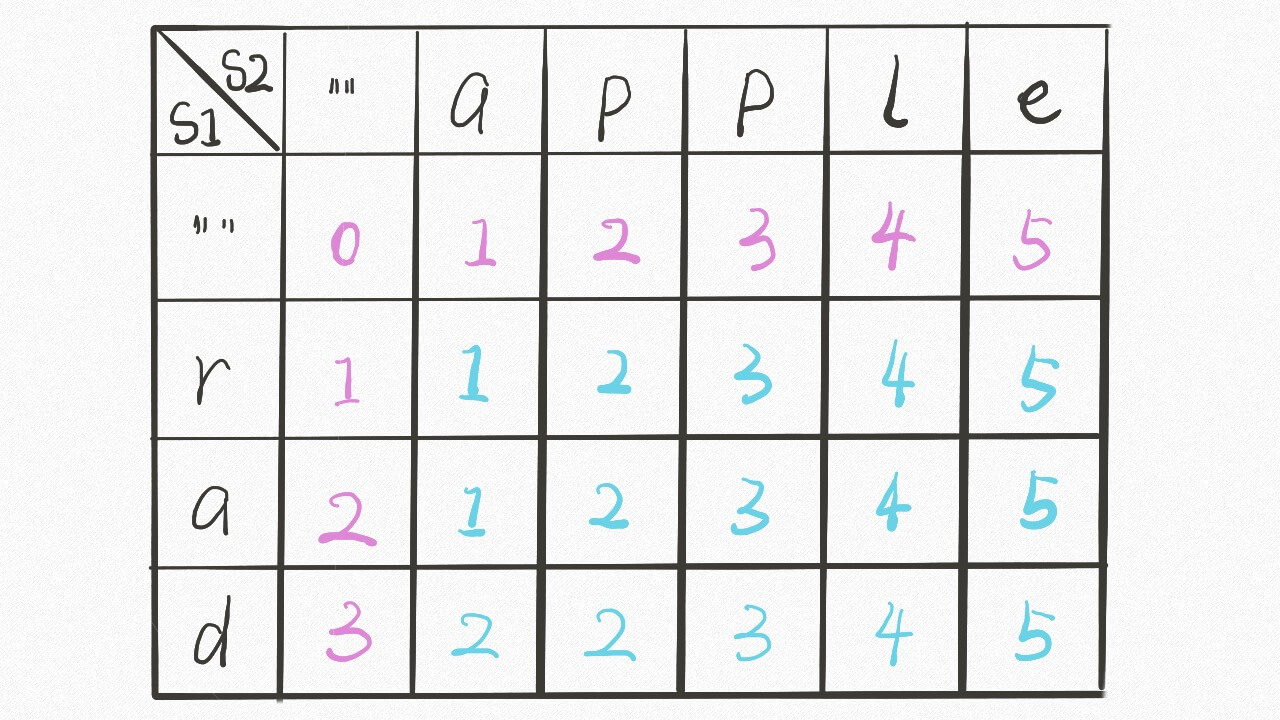
• dp table
• dp[i] [j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2的最近编辑距离

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        len1, len2 = len(word1), len(word2)
        dp = [[0 for _ in range(len2+1)] for _ in range(len1+1)]
        for i in range(len1+1):
            dp[i][0] = i
        for j in range(len2+1):
            dp[0][j] = j
            
        for i in range(1, len1+1):
            for j in range(1, len2+1):
                if word1[i-1]==word2[j-1]:
                    dp[i][j]=dp[i-1][j-1]
                else:
                    dp[i][j]=min(
                        dp[i][j-1]+1, dp[i-1][j]+1, dp[i-1][j-1]+1
                    )
        return dp[-1][-1]

cpp

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n1 = word1.size(), n2 = word2.size();

        vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));
        for (int i = 0; i <= n1; ++i) dp[i][0] = i;
        for (int j = 0; j <= n2; ++j) dp[0][j] = j;

        for (int i = 1; i <= n1; ++i) {
            for (int j = 1; j <= n2; ++j) {
                if (word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
                }
            }
        }
        return dp[n1][n2];
    }
};