887 鸡蛋掉落

本文最后更新于：2022年4月9日 中午

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

示例 1：

1
2
3
4
5
6
7
输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

示例 2：

1
2
输入：K = 2, N = 6
输出：3

示例 3：

1
2
输入：K = 3, N = 14
输出：4

提示：

  1. 1 <= K <= 100
  2. 1 <= N <= 10000

Solution

参考：《算法小抄》2.12

  • 定义问题状态——> 有什么选择 ——> 穷举
  • 时间复杂度 O(KN^2^)，超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# @lc code=start
class Solution:
    def superEggDrop(self, K: int, N: int) -> int:
        memo=dict()
        def dp(K, N):
            if N==0: return 0
            if K==1: return N
            if( K, N) in memo:
                return memo[(K,N)]
            res = float('inf')
            for i in range(1,N+1):
                res = min(res, max(dp(K,N-i), dp(K-1, i-1))+1)
            memo[(K, N)]=res
            return res
        return dp(K, N)
# @lc code=end
  • 动态规划+二分搜索，本质同上解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def superEggDrop(self, K: int, N: int) -> int:
        memo=dict()
        def dp(K, N):
            if N==0: return 0
            if K==1: return N
            if( K, N) in memo:
                return memo[(K,N)]
            res = float('inf')
            low, high = 1,N
            while low<=high:
                mid = low+(high-low)//2
                broken = dp(K-1, mid-1)
                not_broken = dp(K, N-mid)
                if broken>not_broken:
                    high=mid-1
                    res=min(res,broken+1)
                else:
                    low=mid+1
                    res=min(res,not_broken+1)
            memo[(K,N)]=res
            return res
        return dp(K,N)

  • 定义 dp table：确定当前的鸡蛋个数和最多允许的扔鸡蛋次数，就能够确定最高楼层数

  • dp[k] [n] = m 当前状态为 k 个鸡蛋，面对 n 层楼，这个状态下最少的扔鸡蛋次数为 m

  • while 循环结束的条件是 dp[K][m] == N，也就是 给你 K 个鸡蛋，测试 m 次，最坏情况下最多能测试 N 层楼。

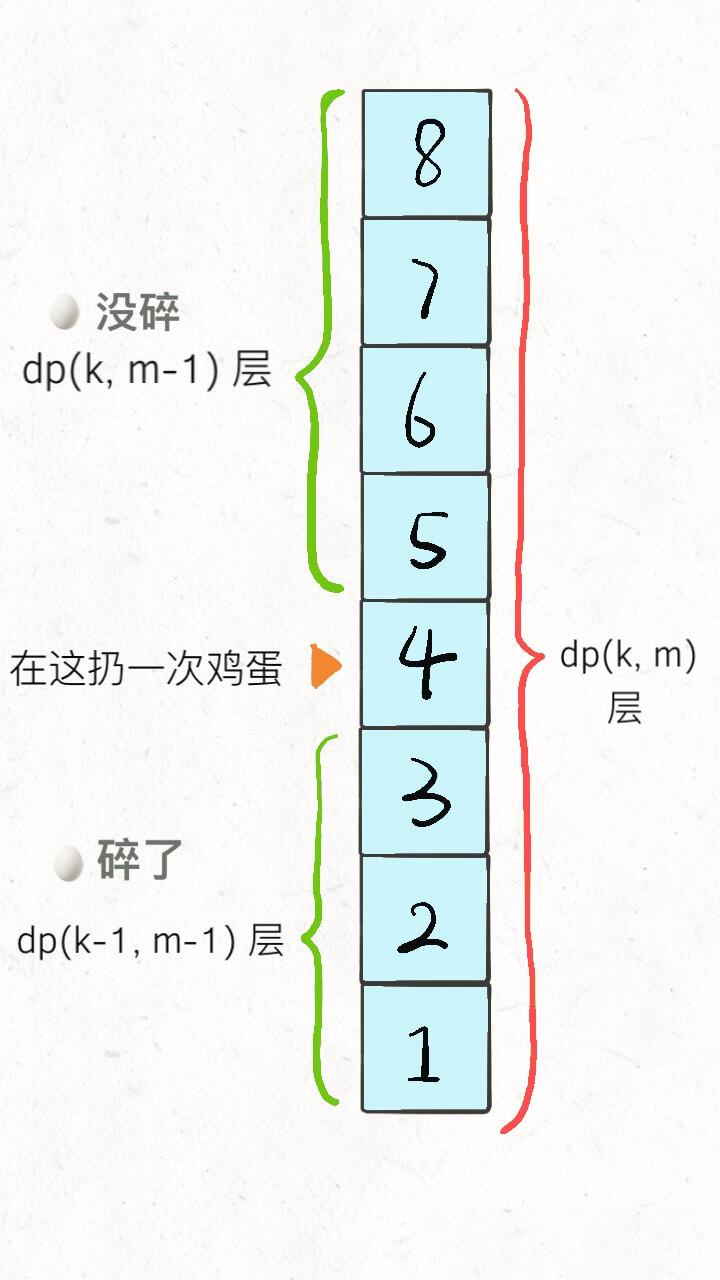
  • dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1

    dp[k] [m - 1] 就是楼上的楼层数，因为鸡蛋个数 k 不变，也就是鸡蛋没碎，扔鸡蛋次数 m 减一；

    dp[k - 1] [m - 1] 就是楼下的楼层数，因为鸡蛋个数 k 减一，也就是鸡蛋碎了，同时扔鸡蛋次数 m 减一。

参考：《算法小抄》2.13

img 
1
2
3
4
5
6
7
8
9
class Solution:
    def superEggDrop(self, K: int, N: int) -> int:
        dp = [[0 for _ in range(N+2)] for _ in range(K+2)]
        m=0
        while dp[K][m]<N:
            m+=1
            for k in range(1,K+1):
                dp[k][m]=dp[k][m-1]+dp[k-1][m-1]+1
        return m

cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int superEggDrop(int k, int n) {
        vector<vector<int>> dp(k+1, vector<int>(n+1, 0));
        int m = 0;
        while (dp[k][m] < n) {
            m++;
            for (int i = 1; i <= k; ++i) {
                dp[i][m] = dp[i-1][m-1] + dp[i][m-1] + 1;
            }
        }

        return m;
    }
};