450 删除二叉搜索树中的节点

本文最后更新于：2022年9月21日 凌晨

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

  1. 首先找到需要删除的节点；
  2. 如果找到了，删除它。

说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。

    5
   / \
  2   6
   \   \
    4   7

Solution

参考：《算法小抄》3.4

  • 删除一个节点有三种情形：
    1. 该节点左右子节点都为空，直接删除
    2. 该节点有一个非空子节点，让这个孩子直接接替
    3. 该节点有两个子节点，可以选择让右子树中的最小节点来代替
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# @lc code=start
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root: return
        if root.val==key:
            if not root.left: return root.right
            if not root.right: return root.left
            minNode = self.getMinNode(root.right)
            root.val = minNode.val
            root.right = self.deleteNode(root.right, minNode.val)
        elif root.val < key:
            root.right = self.deleteNode(root.right, key)
        elif root.val > key:
            root.left = self.deleteNode(root.left, key)
        return root
            
    def getMinNode(self, root):
        while root.left:
            root = root.left
        return root
# @lc code=end

cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root==nullptr) return root;

        if(root->val < key){
            root->right = deleteNode(root->right, key);
            return root;
        } else if(root->val > key){
            root->left = deleteNode(root->left, key);
            return root;
        } else {
            if(root->left==nullptr)
                return root->right;
            if(root->right==nullptr)
                return root->left;
            TreeNode* successor = new TreeNode(getMin(root->right)->val);
            successor->right = removeMin(root->right);
            successor->left = root->left;
            return successor;
        }
    }

    TreeNode* getMin(TreeNode* root){
        while(root->left){
            root = root->left;
        }
        return root;
    }

    TreeNode* removeMin(TreeNode* root){
        if(root->left==nullptr){
            TreeNode* rightNode = root->right;
            delete root;
            return rightNode;
        }
        root->left = removeMin(root->left);
        return root;
    }
};
// @lc code=end
  • removeMin 的迭代写法
1
2
3
4
5
6
7
8
9
10
11
12
13
TreeNode* removeMin(TreeNode* root) {
    TreeNode* cur = root, *pre = nullptr;
    while (cur->left) {
        pre = cur;
        cur = cur->left;
    }
    if (pre){
        pre->left = cur->right;
        return root;
    }
    else 
        return root->right;
}

参考 代码随想录 ，另一种替代方法

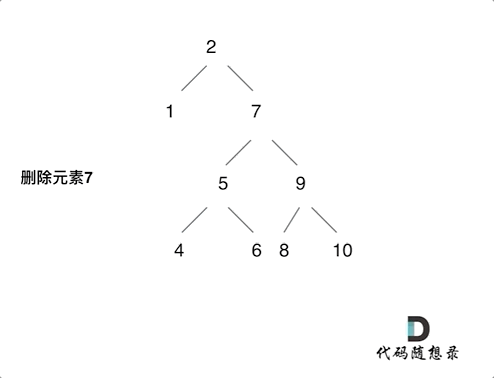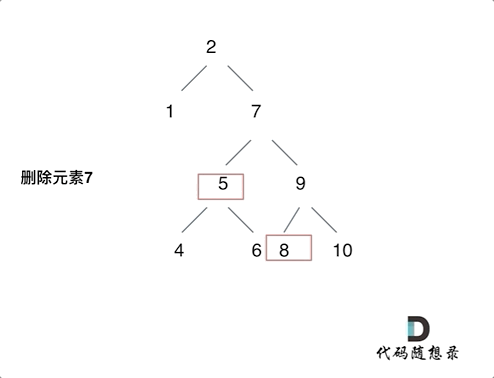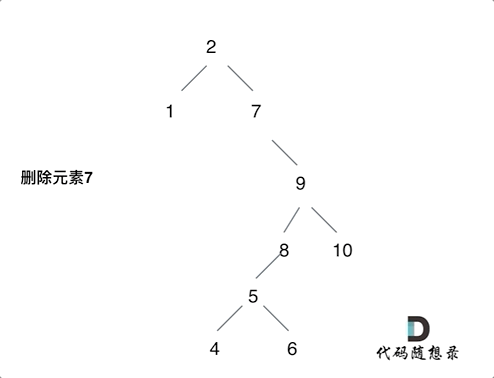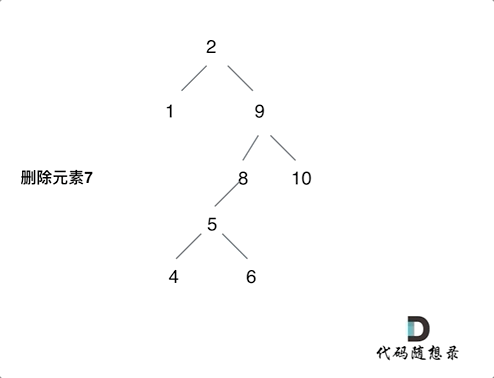
  • 对于左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。图片 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        if (root->val == key) {
            if (root->left == nullptr) return root->right; 
            else if (root->right == nullptr) return root->left; 
            else {  
                TreeNode* cur = root->right; // 找右子树最左面的节点
                while(cur->left != nullptr) { 
                    cur = cur->left;
                }
                // 把要删除的节点（root）左子树放在cur的左孩子的位置
                cur->left = root->left; 
                TreeNode* tmp = root; 
                root = root->right;
                delete tmp;
                return root;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return root;
        }
        if (root.val == key) {
            if (root.left == null && root.right == null) {
                return null;
            }
            if (root.left == null || root.right == null) {
                return root.left == null ? root.right : root.left;
            }
            // 左右子树都不为空
            TreeNode node = root.right;
            while (node.left != null) {
                node = node.left;
            }
            node.left = root.left;
            root.left = null;
            return root.right;
        }

        if (root.val > key) {
            root.left = deleteNode(root.left, key);
        }
        if (root.val < key) {
            root.right = deleteNode(root.right, key);
        }

        return root;
    }
}