给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

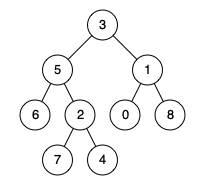
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

Solution

参考：《算法小抄》3.6 、代码随想录

• 递归法
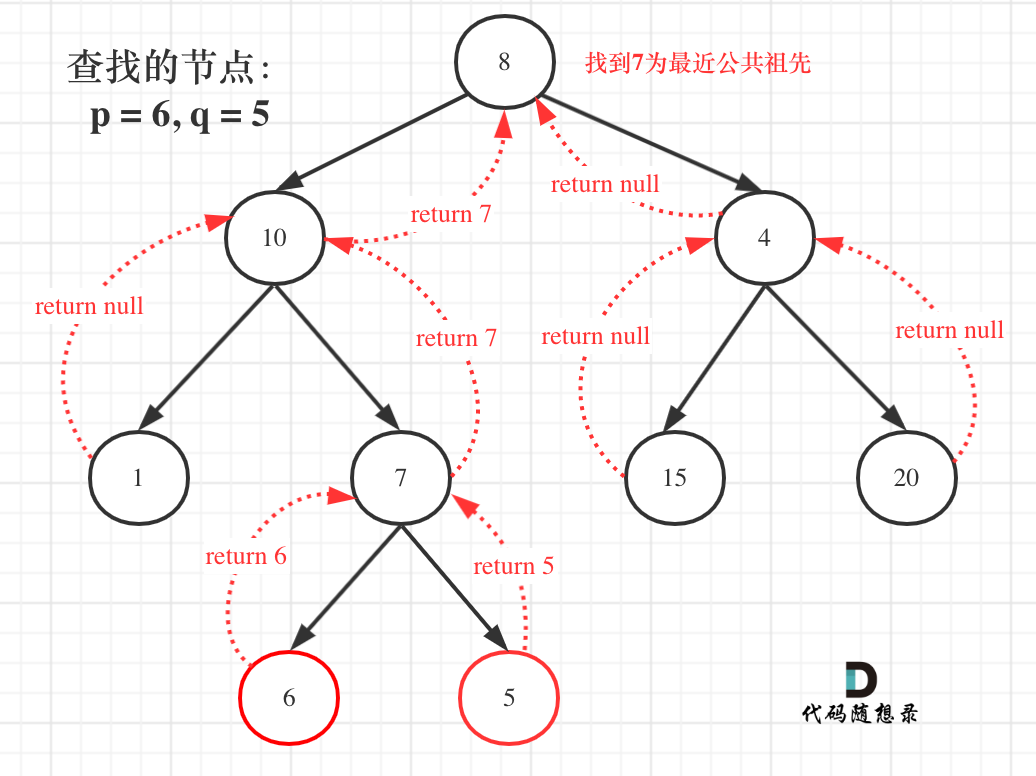
• 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。
• 在回溯的过程中，必然要遍历整颗二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
• 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

# @lc code=start
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return
        if root==p or root== q: return root
        
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p,q)
        
        if left and right:
            return root
        if not left and not right:
            return
        return left if left else right
# @lc code=end

cpp

// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr) return nullptr;
        if(root==p || root==q) return root;

        TreeNode* leftNode = lowestCommonAncestor(root->left, p, q);
        TreeNode* rightNode = lowestCommonAncestor(root->right, p, q);

        // p 和 q 都在以 root 为根的树中
        if(leftNode!=nullptr && rightNode!=nullptr)
            return root;
        // p 和 q 都不在以 root 为根的树中
        if(leftNode==nullptr && rightNode==nullptr)
            return nullptr;
        // p 和 q 只有一个在以 root 为根的树中，返回该节点
        return leftNode==nullptr ? rightNode : leftNode;
    }
};
// @lc code=end

注：如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

「在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回；如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）」

搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;