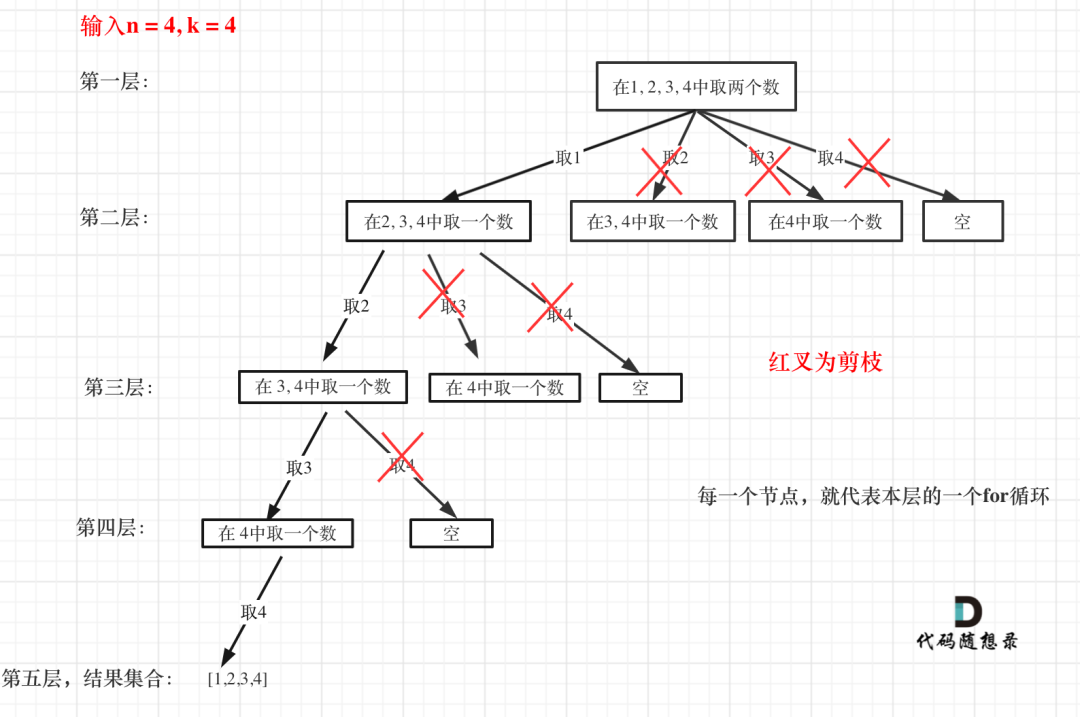
给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

Solution

参考：《算法小抄》4.1 、[78 子集](78 子集.md)

• 回溯法

# @lc code=start
class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        if n<=0 or k<=0: return 
        res = []
        tarck = []
        def backtrack(n, k, start, tarck):
            if k==len(tarck):
                res.append(tarck[:])
            for i in range(start, n+1):
                tarck.append(i)
                backtrack(n, k, i+1, tarck)
                tarck.pop()
        backtrack(n, k, 1, tarck)
        return res
# @lc code=end

cpp

// @lc code=start
class Solution {
private:
    vector<vector<int>> res;

    void dfs(int n, int k, int start, vector<int>& cur){
        if(cur.size()==k){
            res.push_back(cur);
            return;
        }

        for(int i=start; i<=n; ++i){
            cur.push_back(i);
            dfs(n, k, i+1, cur);
            cur.pop_back();
        }
        return;
    }

public:
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        if(n<=0 || k<=0 || k>n)
            return res;

        vector<int> cur;
        dfs(n, k, 1, cur);
        return res;
    }
};
// @lc code=end

• 剪枝优化，参考 代码随想录

class Solution {
private:
    vector<vector<int>> res;

    void dfs(int n, int k, int start, vector<int>& cur){
        if(cur.size()==k){
            res.push_back(cur);
            return;
        }

        for(int i=start; i<=n-(k-cur.size())+1; ++i){
            cur.push_back(i);
            dfs(n, k, i+1, cur);
            cur.pop_back();
        }
        return;
    }

public:
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        if(n<=0 || k<=0 || k>n)
            return res;

        vector<int> cur;
        dfs(n, k, 1, cur);
        return res;
    }
};

java

class Solution {
    List<List<Integer>> result;
    List<Integer> path;

    public List<List<Integer>> combine(int n, int k) {
        result = new ArrayList<>();
        path = new ArrayList<>();
        backtrack(n, k, 1);
        return result;
    }

    private void backtrack(int n, int k, int start) {
        if (path.size() == k) {
            // 这里一定要采用深拷贝
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = start; i <= n - (k - path.size()) + 1; ++i) {
            path.add(i);
            backtrack(n, k, i + 1);
            path.remove(path.size() - 1);
        }
    }
}