给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

Solution

参考：《算法小抄》4.1 、**@lei-hou-ya**

• 迭代法
• 每次添加一个元素，都是在前面元素的基础之上，每个集合都在末尾添加这个元素，生成一个新的集合，再把新的集合添加到原来的集合当中，如[[1]]，再添加2：[[1],[1,2]]

# @lc code=start
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        s = [[]]
        if not nums:
            return 
        for i in nums:
            size = len(s)
            for j in range(size):
                pre = s[j].copy()
                pre.append(i)
                s.append(pre)
        return s
# @lc code=end

cpp

// @lc code=start
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        if(nums.size()==0)
            return {{}};
        
        // 把最后一个元素取出
        int n = nums.back();
        nums.pop_back();
        // 递归得出前面元素的所有子集
		vector<vector<int>> res = subsets(nums);
        
        int size = res.size();
        for(int i=0; i<size; ++i){
            res.push_back(res[i]);
            res.back().push_back(n);
        }
        return res;
    }
};
// @lc code=end

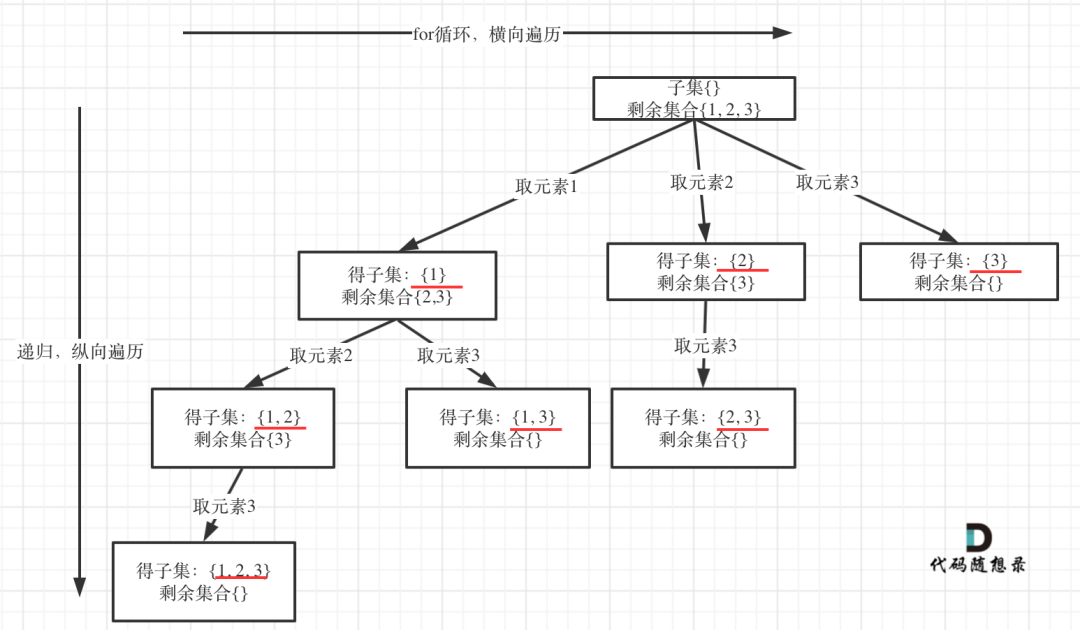
• 回溯法，参考 代码随想录
• 不需要加终止条件，因为当 index >= nums.size()，本层for循环本来也结束了
• 「求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树」

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        if not nums:
            return 
        track = []
        def backtrack(nums, start, track):
            res.append(track[:])
            for i in range(start, len(nums)):
                track.append(nums[i])
                backtrack(nums, i+1, track)
                track.pop()
        backtrack(nums, 0, track)        
        return res

cpp

// @lc code=start
class Solution {
private:
    vector<vector<int>> res;

    void dfs(vector<int>& nums, int index, vector<int>& cur){
        res.push_back(cur);

        for(int i=index; i<nums.size(); ++i){
            cur.push_back(nums[i]);
            dfs(nums, i+1, cur);
            cur.pop_back();
        }
        return;
    }

public:
    vector<vector<int>> subsets(vector<int>& nums) {
        res.clear();
        if(nums.size()==0)
            return res;
        vector<int> cur;
        dfs(nums, 0, cur);
        return res;
    }
};
// @lc code=end

注：子集问题和组合问题、分割问题的的区别

• 子集 是收集树形结构中树的所有节点的结果
• 组合问题、分割问题 是收集树形结构中叶子节点的结果