42 接雨水

本文最后更新于：2022年4月9日 中午

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

img

1
2
3
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

1
2
输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length
  • 0 <= n <= 3 * 104
  • 0 <= height[i] <= 105

Solution

参考：《算法小抄》5.4 

1
2
3
4
5
6
7
8
9
10
11
# @lc code=start
class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        for i in range(1,n-1):
            lmax = max(height[:i+1])
            rmax = max(height[i:])
            ans += min(lmax, rmax) - height[i]
        return ans
# @lc code=end
  • 备忘录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        if (n <= 2) return 0;

        vector<int> left(n, 0);
        vector<int> right(n, 0);
        left[0] = height[0], right[n-1] = height[n-1];
        for (int i = 1; i < n; ++i) {
            left[i] = max(left[i-1], height[i]);
        }
        for (int i = n-2; i >=0; --i) {
            right[i] = max(right[i+1], height[i]);
        }

        int sum = 0;
        for (int i = 0; i < n; ++i) {
            sum += min(left[i], right[i]) - height[i];
        }
        return sum;
    }
};

  • 双指针

  • l_max 是 height[0..left] 中最高柱子的高度，r_max 是 height[right..end] 的最高柱子的高度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def trap(self, height: List[int]) -> int:
        if not height: return 0
        n = len(height)
        ans = 0
        left, right = 0, n-1
        lmax, rmax = height[0], height[n-1]
        
        while left<right:
            lmax = max(lmax, height[left])
            rmax = max(rmax, height[right])
            if lmax<rmax:
                ans+=lmax-height[left]
                left+=1
            else:
                ans+=rmax-height[right]
                right-=1
        return ans

  • 单调栈，参考代码随想录

  • 从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

图片

整体代码

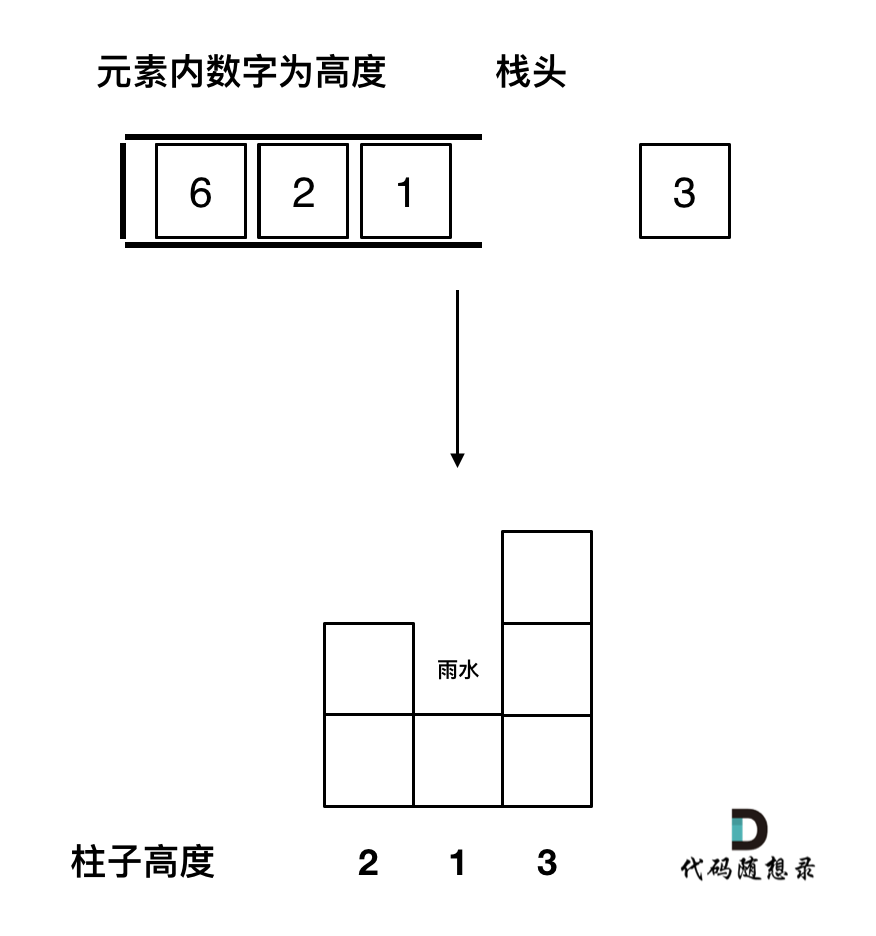
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0; // 可以不加
        stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
        st.push(0);
        int sum = 0;
        for (int i = 1; i < height.size(); i++) {
            if (height[i] < height[st.top()]) {     // 情况一
                st.push(i);
            } if (height[i] == height[st.top()]) {  // 情况二
                st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。
                st.push(i);
            } else {                                // 情况三
                while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
                    int mid = st.top();
                    st.pop();
                    if (!st.empty()) {
                        int h = min(height[st.top()], height[i]) - height[mid];
                        int w = i - st.top() - 1; // 注意减一，只求中间宽度
                        sum += h * w;
                    }
                }
                st.push(i);
            }
        }
        return sum;
    }
};

精简版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() == 0) return 0;
        int res = 0;
        stack<int> st;  // 单调栈，从小到大，保存元素下标
        st.push(0);
        for (int i = 1; i < height.size(); ++i) {
            while (!st.empty() && height[i] > height[st.top()]) {
                int mid = height[st.top()];
                st.pop();
                if (!st.empty()) {
                    int h = min(height[i], height[st.top()]) - mid;
                    int w = i - st.top() - 1;
                    res += h * w;
                }
            }
            st.push(i);
        }
        return res;
    }
};