给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:

假设你总是可以到达数组的最后一个位置。

Solution

参考：《算法小抄》5.7 、**@LeetCode官方**

• 贪心算法

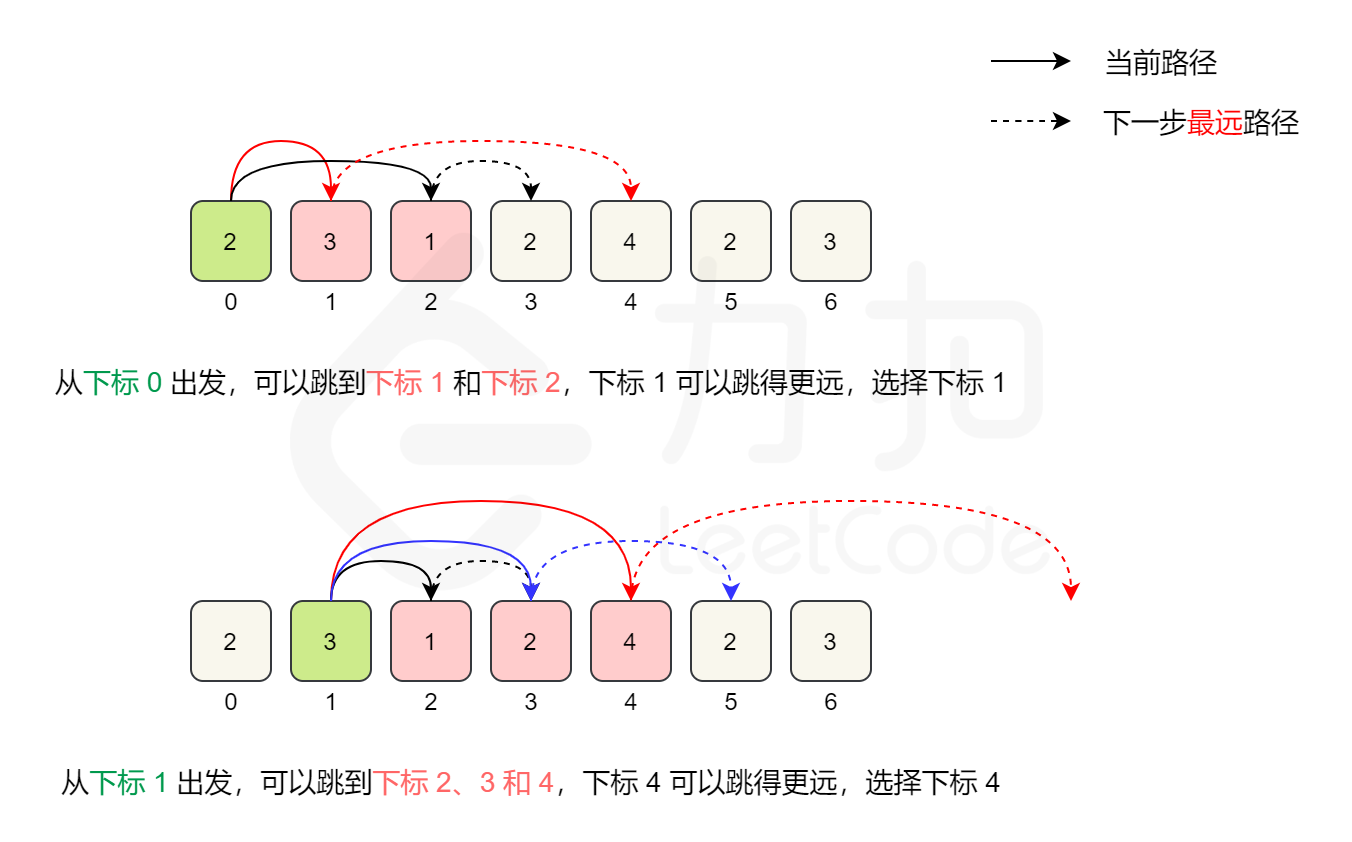
在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。如果访问最后一个元素，在边界正好为最后一个位置的情况下，我们会增加一次「不必要的跳跃次数」，因此我们不必访问最后一个元素。

class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        # 从索引 i，最多能跳到索引 end
        end = 0
        # 从索引 [i:end] 起跳，最远能到达的距离
        farthest = 0
        cnt = 0
        for i in range(n-1):
            farthest = max(nums[i]+i, farthest)
            if end==i:
                cnt += 1
                end = farthest
        return cnt

cpp

// @lc code=start
class Solution {
public:
    int jump(vector<int>& nums) {
        int fastest = 0;
        int end = 0;
        int cnt = 0;

        for (int i = 0; i < nums.size() - 1; ++i) {
            fastest = max(fastest, i + nums[i]);
            if (end == i) {
                cnt++;
                end = fastest;
            }
        }
        return cnt;
    }
};
// @lc code=end

• 动态规划，超时

# @lc code=start
class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        # 从 0 跳到 n-1 不会超过 n-1 步
        memo = [n]*n
        
        # 返回从索引 p 跳到最后一格需要的最小步数
        def dp(nums, p):
            n = len(nums)
            if p>=n-1:
                return 0
            if memo[p] != n:
                return memo[p]
            step = nums[p]
            for i in range(1, step+1):
                sub = dp(nums, p+i)
                memo[p] = min(memo[p], sub+1)
            return memo[p]
        return dp(nums, 0)
# @lc code=end