319 灯泡开关

本文最后更新于：2022年4月9日 中午

初始时有 n 个灯泡关闭。

第 1 轮，你打开所有的灯泡。 第 2 轮，每两个灯泡你关闭一次。 第 3 轮，每三个灯泡切换一次开关（如果关闭则开启，如果开启则关闭）。

第 i 轮，每 i 个灯泡切换一次开关。 对于第 n 轮，你只切换最后一个灯泡的开关。

找出 n 轮后有多少个亮着的灯泡。

示例 1：

img 
1
2
3
4
5
6
7
8
9
输入：n = 3
输出：1 
解释：
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭]. 

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

1
2
输入：n = 0
输出：0

示例 3：

1
2
输入：n = 1
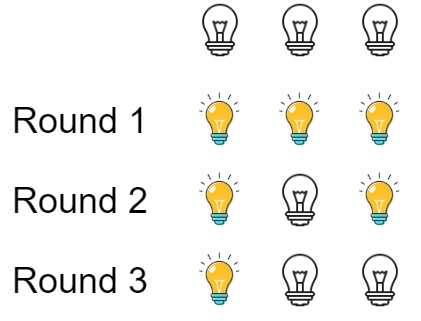
输出：1

提示：

  • 0 <= n <= 109

Solution

参考：《算法小抄》5.13

我们假设只有 6 盏灯，而且我们只看第 6 盏灯。需要进行 6 轮操作对吧，请问对于第 6 盏灯，会被按下几次开关呢？这不难得出，第 1 轮会被按，第 2 轮，第 3 轮，第 6 轮都会被按。

为什么第 1、2、3、6 轮会被按呢？因为 6=1*6=2*3。一般情况下，因子都是成对出现的，也就是说开关被按的次数一般是偶数次。但是有特殊情况，比如说总共有 16 盏灯，那么第 16 盏灯会被按几次?

16=1*16=2*8=4*4

其中因子 4 重复出现，所以第 16 盏灯会被按 5 次，奇数次。

我们求 16 的平方根，等于 4，这就说明最后会有 4 盏灯亮着，它们分别是第 1*1=1 盏、第 2*2=4 盏、第 3*3=9 盏和第 4*4=16 盏。

1
2
3
4
5
# @lc code=start
class Solution:
    def bulbSwitch(self, n: int) -> int:
        return int(math.sqrt(n))
# @lc code=end
algo leetcode 算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！