给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。

示例 1:

输入: [[1,1],[2,2],[3,3]]
输出: 3
解释:
^
|
|        o
|     o
|  o  
+------------->
0  1  2  3  4

示例 2:

输入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出: 4
解释:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

Solution

参考 likou-50 、windliang

用 HashMap 去计数，斜率作为 key，然后遍历平面上的其他点，相同的 key 意味着在同一条直线上。

• 斜率是小数，怎么办

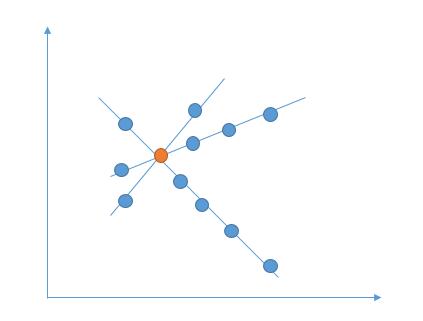
用分数去表示，求分子分母的最大公约数，然后约分，最后将 「分子 + “/“ + “分母”」作为 key 即可。

• 重叠的点如何处理

当确定某个点的时候，平面内如果有和这个重叠的点，如果按照正常的算法约分的话，会出现除 0 的情况，所以我们需要单独用一个变量记录重叠点的个数，而重叠点一定是过当前点的直线的。

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        if(points.size()<3) 
            return points.size();
        int res = 0;
        for(int i=0; i<points.size(); ++i){
            int duplicate=0;
            int curMax=0;
            unordered_map<string,int> oneline;
            for(int j=i+1; j<points.size(); ++j){
                if(points[i][0]==points[j][0] && points[i][1]==points[j][1]){
                    duplicate += 1;
                    continue;
                }

                int diffX = points[j][0]-points[i][0];
                int diffY = points[j][1]-points[i][1];
                int temp = gcd(diffX, diffY);
                string key = to_string(diffX/temp)+'/'+to_string(diffY/temp);
                oneline[key] += 1;
                curMax = max(curMax, oneline[key]);
            }
            res = max(res, curMax+duplicate+1);
        }
        return res;
    }
private:
    int gcd(int a, int b){
        if(b==0)
            return a;
        return gcd(b, a%b);
    }
};