给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

• 1 <= n <= 104

Solution

参考 liuyubobobo 的解题思路。

转化为求一个无权图中从 n 到 0 的最短路径。

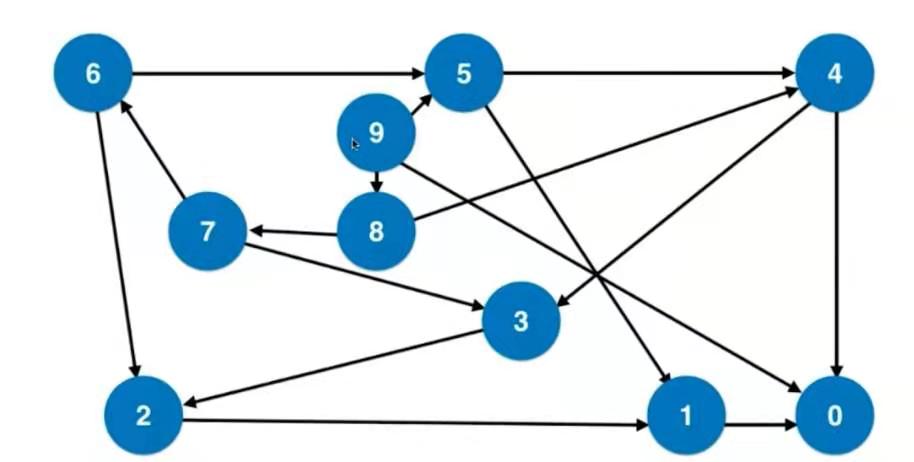
• BFS，超时
• 时间复杂度 O(2^n^ )，空间复杂度 O(2^n^ )

// @lc code=start
class Solution {
public:
    int numSquares(int n) {
        queue<pair<int,int>> q;
        q.push(make_pair(n,0));
        
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();
            if(num == 0)
                return step;
            // BFS
            for(int i=1; num-i*i >= 0; ++i)
                q.push(make_pair(num-i*i, step+1));
        }
        return -1; // 表示没找到
    }
};
// @lc code=end

• BFS，借助备忘录优化
• 时间复杂度 O(n)，空间复杂度 O(n)

class Solution {
public:
    int numSquares(int n) {
        queue<pair<int,int>> q;
        q.push(make_pair(n,0));

        // 备忘录记录访问过的数据
        vector<bool> visited(n+1, false);
        visited[n] = true;
        
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();
            if(num == 0)
                return step;
            // BFS
            for(int i=1; num-i*i >= 0; ++i){
                if(!visited[num-i*i]){
                    q.push(make_pair(num-i*i, step+1));
                    visited[num-i*i] = true;
                }
            }
        }
        return -1; // 表示没找到
    }
};

• BFS，借助备忘录优化，早停
• 时间复杂度 O(n)，空间复杂度 O(n)

class Solution {
public:
    int numSquares(int n) {
        queue<pair<int,int>> q;
        q.push(make_pair(n,0));

        // 备忘录记录访问过的数据
        vector<bool> visited(n+1, false);
        visited[n] = true;
        
        while(!q.empty()){
            int num = q.front().first;
            int step = q.front().second;
            q.pop();

            // BFS
            for(int i=1; num-i*i >= 0; ++i){
                if(!visited[num-i*i]){
                    if(num-i*i == 0) return step+1;  // 早停
                    q.push(make_pair(num-i*i, step+1));
                    visited[num-i*i] = true;
                }
            }
        }
        return -1; // 表示没找到
    }
};

动态规划

• 记忆化搜索

class Solution {
private:
    vector<int> memo;

    int go(int n){
        if(n==0)
            return 0;
        if(memo[n] != -1)
            return memo[n];
        
        int res = INT_MAX;
        for(int i=1; n-i*i>=0; ++i){
            res = min(res, 1+go(n-i*i));
        }
        memo[n] = res;
        return res;
    }

public:
    int numSquares(int n) {
        memo = vector<int>(n+1, -1);
        return go(n);
    }
};

• 借助 dp 数组

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1, INT_MAX);
        dp[0] = 0;
        for(int i=1; i<=n; ++i){
            for(int j=1; i-j*j>=0; ++j){
                dp[i] = min(dp[i], 1+dp[i-j*j]);
            }
        }
        return dp[n];
    }
};