108 将有序数组转换为二叉搜索树

本文最后更新于：2022年4月9日 中午

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
9
给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

Solution

参考 LeetCode官方 题解，代码随想录

图片
  • 在给定中序遍历序列数组的情况下，每一个子树中的数字在数组中一定是连续的，因此可以通过数组下标范围确定子树包含的数字，下标范围记为 $[\textit{left}, \textit{right}]$。对于整个中序遍历序列，下标范围从$ left=0$ 到 $\textit{right}=\text{nums.length}-1$。当 $\textit{left}>\textit{right}$ 时，平衡二叉搜索树为空。
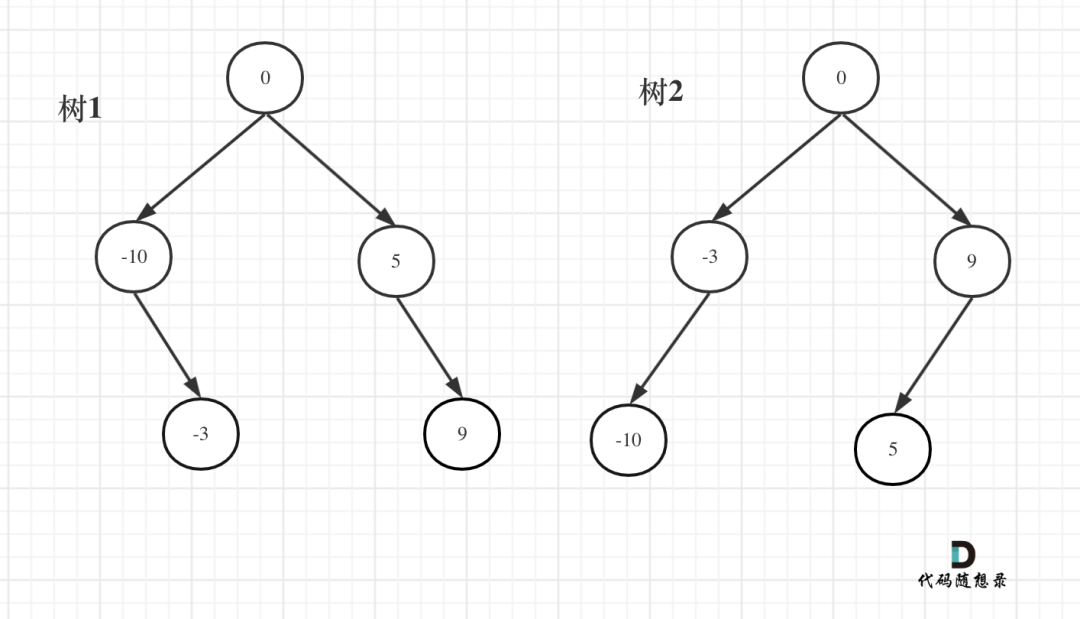
  • 构造结果 [0,-10,5,null,-3,null,9]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right){
        if(left>right) return nullptr;

        int mid = left + ((right - left) / 2);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid-1);
        root->right = helper(nums, mid+1, right);
        return root;
    }
};
// @lc code=end
  • 定义下标范围从$ left=0$ 到 $\textit{right}=\text{nums.length}$。左闭右开
  • 构造结果 [0,-3,9,-10,null,5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size());
    }
private:
    TreeNode* helper(const vector<int>& nums, int left, int right) {
        if (left >= right) return nullptr;

        int mid = left + ((right - left) / 2);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid);
        root->right = helper(nums, mid+1, right);
        return root;
    }
};
  • 迭代法
  • 通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下标，一个队列放右区间下标。模拟不断分割的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;

        TreeNode* root = new TreeNode(0);   // 初始根节点
        queue<TreeNode*> nodeQue;           // 放遍历的节点
        queue<int> leftQue;                 // 保存左区间下表
        queue<int> rightQue;                // 保存右区间下表
        nodeQue.push(root);                 // 根节点入队列
        leftQue.push(0);                    // 0为左区间下表初始位置
        rightQue.push(nums.size() - 1);     // nums.size() - 1为右区间下表初始位置

        while (!nodeQue.empty()) {
            TreeNode* curNode = nodeQue.front();
            nodeQue.pop();
            int left = leftQue.front(); leftQue.pop();
            int right = rightQue.front(); rightQue.pop();
            int mid = left + ((right - left) / 2);

            curNode->val = nums[mid];       // 将mid对应的元素给中间节点

            if (left <= mid - 1) {          // 处理左区间
                curNode->left = new TreeNode(0);
                nodeQue.push(curNode->left);
                leftQue.push(left);
                rightQue.push(mid - 1);
            }

            if (right >= mid + 1) {         // 处理右区间
                curNode->right = new TreeNode(0);
                nodeQue.push(curNode->right);
                leftQue.push(mid + 1);
                rightQue.push(right);
            }
        }
        return root;
    }
};