给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

Solution

其他类似题型 [46 全排列]

对比子集问题 [90 子集 II] 的去重逻辑

参考 @liuyubobobo 、 代码随想录

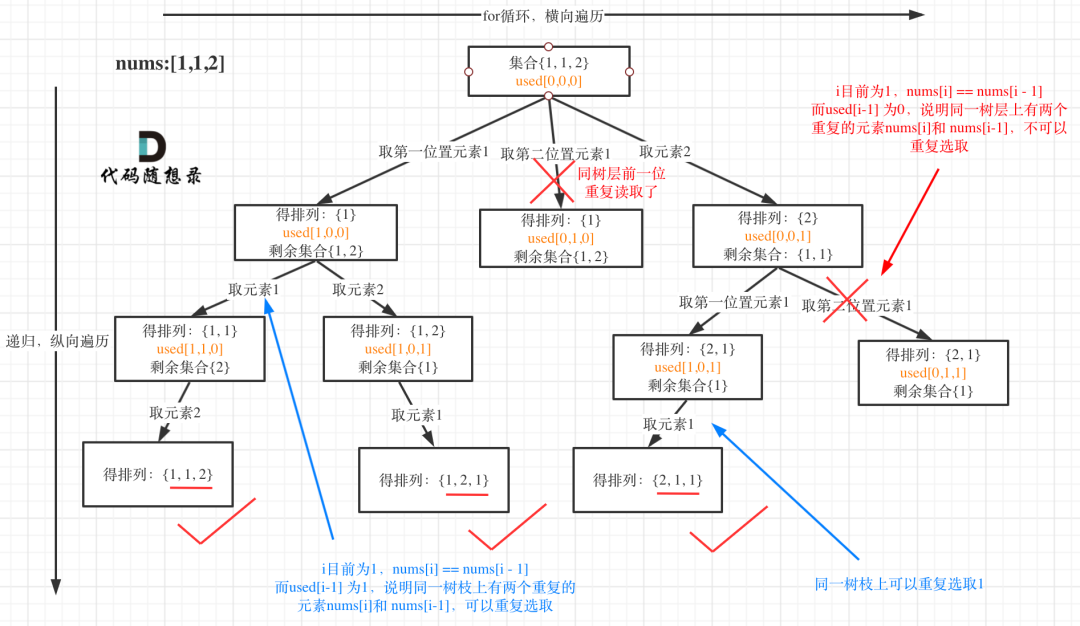
• 回溯法
• 对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。
• 去重一定要对元素进行排序，这样才方便通过相邻的节点来判断是否重复使用了

// @lc code=start
class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        res.clear();
        if (nums.size() == 0) return res;
        sort(nums.begin(), nums.end());
        
        used = vector<bool>(nums.size(), false);
        vector<int> cur;
        backtrack(nums, cur);
        return res;
    }
private:
    vector<vector<int>> res;
    vector<bool> used;

    void backtrack(const vector<int>& nums, vector<int>& cur) {
        if (cur.size() == nums.size()) {
            res.push_back(cur);
            return;
        }

        for (int i = 0; i < nums.size(); ++i) {
            if (!used[i]) {
                // used[i - 1] == true，说明同一树支nums[i - 1]使用过
                // used[i - 1] == false，说明同一树层nums[i - 1]使用过
                if (i > 0 && nums[i] == nums[i-1] && used[i-1] == false)
                    continue;
                used[i] = true;
                cur.push_back(nums[i]);
                backtrack(nums, cur);
                cur.pop_back();
                used[i] = false;
            }
        }
        return;
    }
};
// @lc code=end

拓展：参考 代码随想录

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) { 
    continue;
}

如果改成 used[i - 1] == true， 也是正确的!

「对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！」

举例：[1,1,1]

树层上去重(used[i - 1] == false)，的树形结构如下：

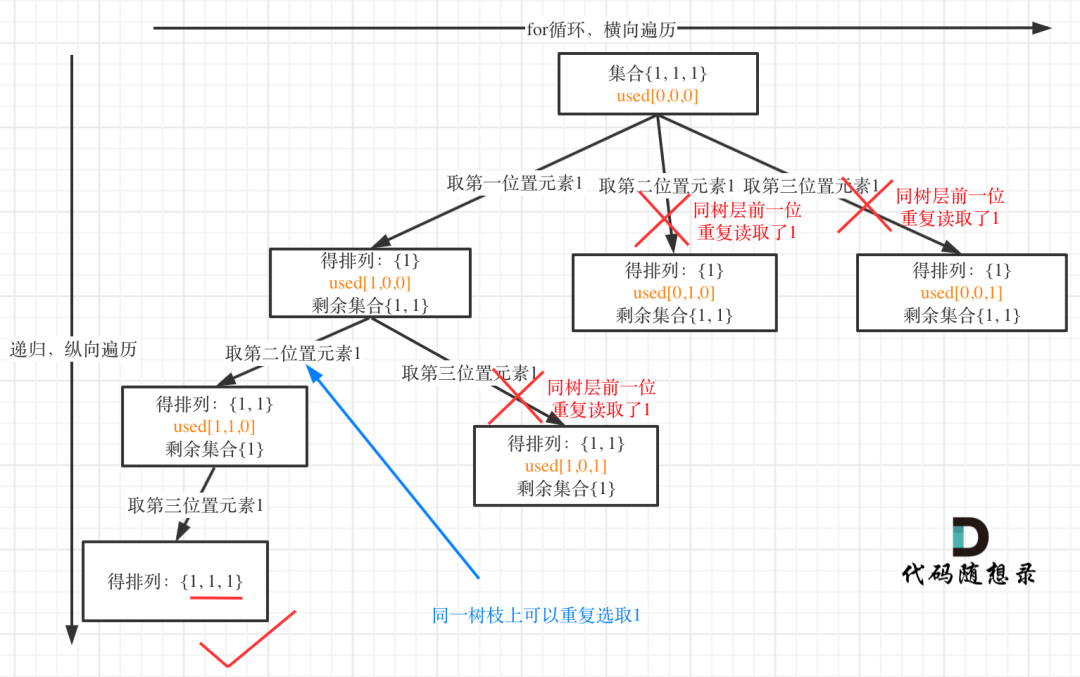
树枝上去重（used[i - 1] == true）的树型结构如下：

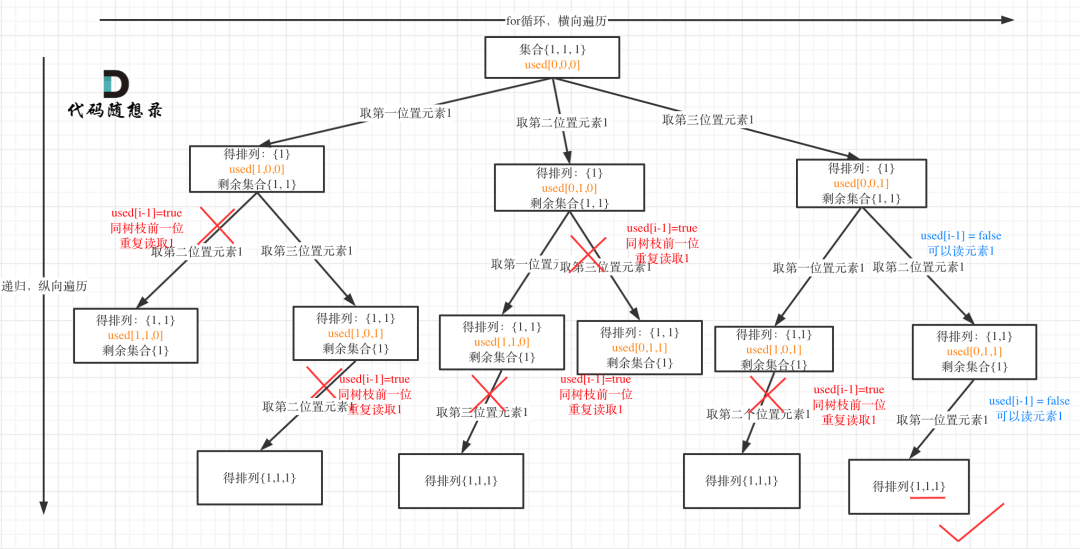
树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。

拓展：性能分析，参考 代码随想录

子集问题分析：

• 时间复杂度：O(n * 2^n )，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2^n)，构造每一组子集都需要填进数组，又需要O(n)，最终时间复杂度：O(n * 2^n)
• 空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)

排列问题分析：

• 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ….. 1 = n!。
• 空间复杂度：O(n)，和子集问题同理。

组合问题分析：

• 时间复杂度：O(n * 2^n)，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
• 空间复杂度：O(n)，和子集问题同理。