52 N皇后 II

本文最后更新于：2022年4月9日 中午

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

img 
1
2
3
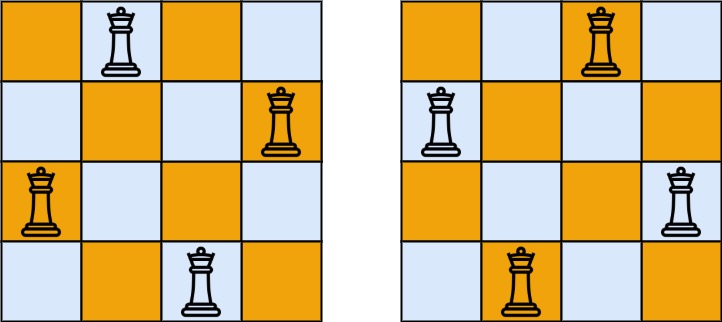
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：1

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

Solution

其他相关题：[51 N皇后]

参考 @liuyubobobo 、**@覃超**、@LeetCode官方

  • 回溯法
  • 加入Queen斜线的限制，加入一个左斜线数组和右斜线数组的判定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// @lc code=start
class Solution {
private:
    void dfs(int& n, vector<bool>& vertical, vector<bool>& left,
                vector<bool>& right, int& count, int row){
        if(row==n){
            ++count;
            return;
        }

        for(int i=0; i<n; ++i){
            if(vertical[i] || left[row+i] || right[row-i+n-1])
                continue;
            vertical[i]=true;
            left[row+i]=true;
            right[row-i+n-1]=true;
            dfs(n, vertical, left, right, count, row+1);
            vertical[i]=false;
            left[row+i]=false;
            right[row-i+n-1]=false;
        }
    }

public:
    int totalNQueens(int n) {
        vector<bool> vertical(n, false);
        vector<bool> left(2*n-1, false);
        vector<bool> right(2*n-1, false);
        int count = 0;
        dfs(n, vertical, left, right, count, 0);
        return count;
    }
};
// @lc code=end
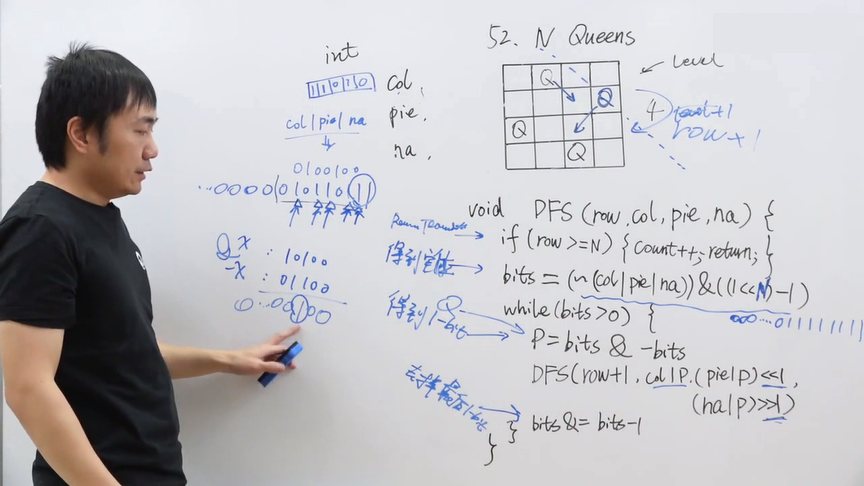
  • 位运算
  • 使用三个整数 columns、diagonals1 和 diagonals 2，分别记录每一列以及两个方向的每条斜线上是否有皇后，每个整数有 N 个二进制位。
  • x & (−x) 可以获得 x 的二进制表示中的最低位的 1 的位置；
  • x & (x-1) 可以将 x 的二进制表示中的最低位的 1 置成 0。

image-20210728183818578

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int totalNQueens(int n) {
        return solve(n, 0, 0, 0, 0);
    }

    int solve(int n, int row, int columns, int diagonals1, int diagonals2) {
        if (row == n) {
            return 1;
        } else {
            int count = 0;
            int availablePos = ((1 << n) - 1) & (~(columns | diagonals1 | diagonals2)); // 得到当前所有的空位
            while (availablePos != 0) {
                int position = availablePos & (-availablePos); // 取最低位的1
                availablePos = availablePos & (availablePos - 1);  // 去掉最低位的1
                count += solve(n, row + 1, columns | position, 
                               (diagonals1 | position) << 1, 
                               (diagonals2 | position) >> 1);
            }
            return count;
        }
    }
};