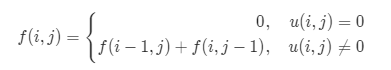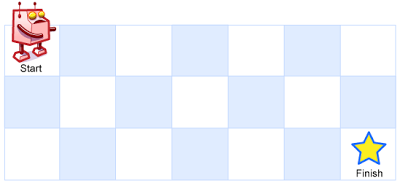
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

Solution

动态规划，参考 @LeetCode官方 、代码随想录

动态规划的题目分为两大类：

• 一种是求最优解类，典型问题是背包问题；
• 另一种就是计数类，比如这里的统计方案数的问题。

它们都存在一定的递推性质。前者的递推性质还有一个名字，叫做 「最优子结构」 ——即当前问题的最优解取决于子问题的最优解，后者类似，当前问题的方案数取决于子问题的方案数。

• 利用 dp 数组

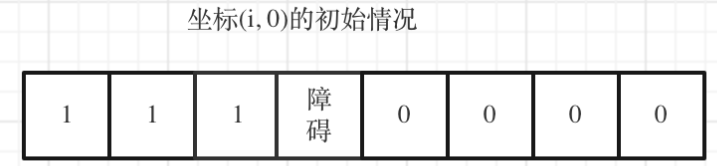
如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i] [0]应该还是初始值0。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        
        // 填充第一行
        for(int i=0; i<n && obstacleGrid[0][i]==0; ++i)
            dp[0][i] = 1;
        // 填充第一列
        for(int j=0; j<m && obstacleGrid[j][0]==0; ++j)
            dp[j][0] = 1;
        // 填充其余
        for(int i=1; i<m; ++i){
            for(int j=1; j<n; ++j){
                if(obstacleGrid[i][j]==1)
                    continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

• 状态压缩
• 注意处理障碍物情况

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<int> dp(n, 0);
        dp[0] = (obstacleGrid[0][0]==0);
        for(int i=0; i<m; ++i){
            for(int j=0; j<n; ++j){
                if(obstacleGrid[i][j]==1){
                    dp[j]=0;
                    continue;
                }
                if(j>0 && obstacleGrid[i][j-1]==0)
                    dp[j] += dp[j-1];
            }
        }
        return dp[n-1];
    }
};