本文最后更新于:2022年4月9日 中午
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
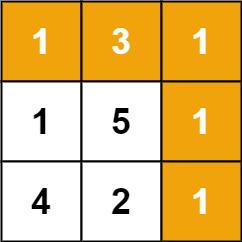
| 输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
|
示例 2:
| 输入:grid = [[1,2,3],[4,5,6]]
输出:12
|
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 100
Solution
动态规划
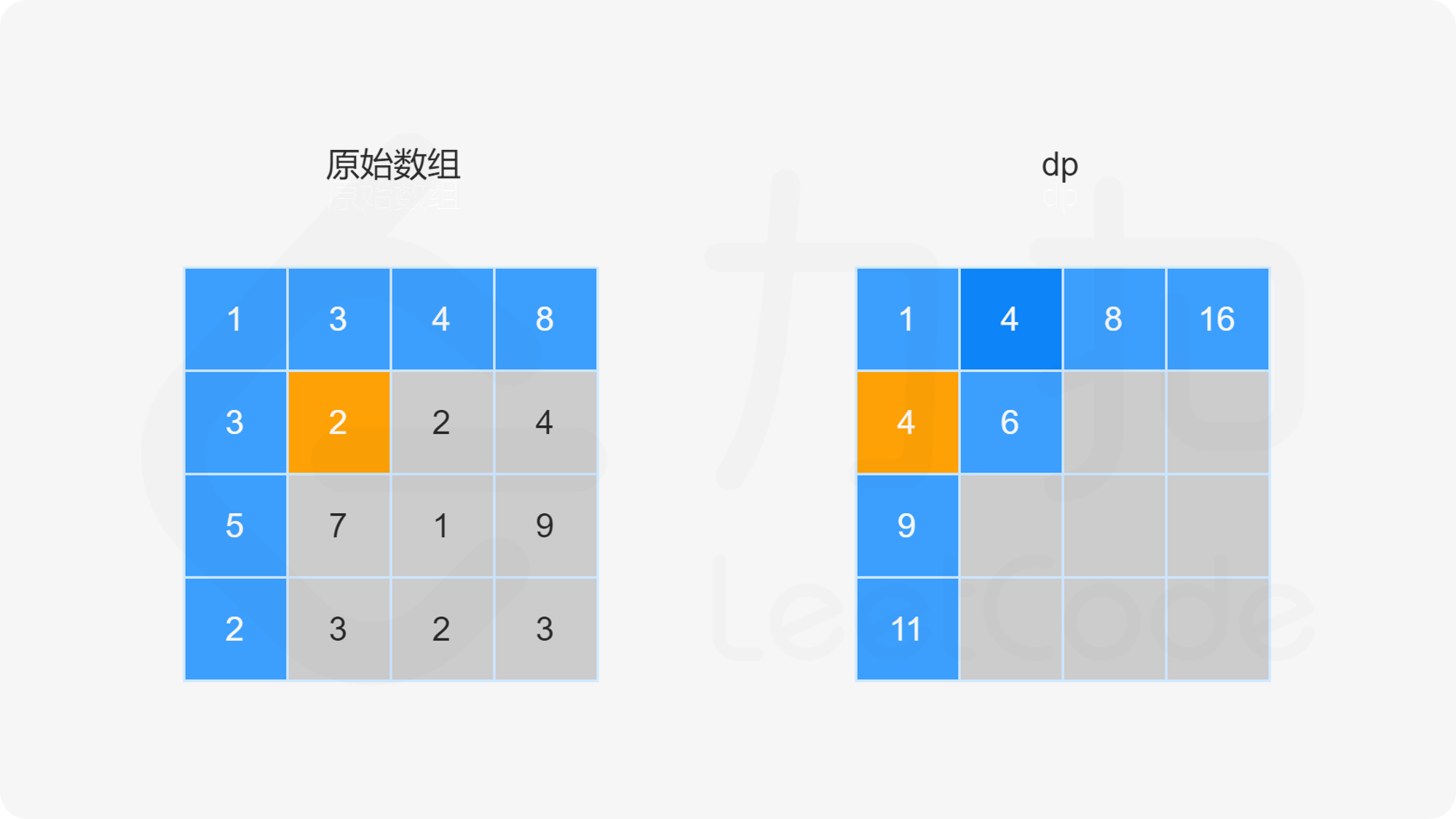
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[0][0] = grid[0][0];
for(int i=1; i<m; ++i)
dp[i][0] = dp[i-1][0]+grid[i][0];
for(int j=1; j<n; ++j)
dp[0][j] = dp[0][j-1]+grid[0][j];
for(int i=1; i<m; ++i){
for(int j=1; j<n; ++j)
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
return dp[m-1][n-1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> dp(n, 0);
dp[0] = grid[0][0];
for(int j=1; j<n; ++j)
dp[j] = grid[0][j] + dp[j-1];
for(int i=1; i<m; ++i){
dp[0] += grid[i][0];
for(int j=1; j<n; ++j){
dp[j] = grid[i][j] + min(dp[j], dp[j-1]);
}
}
return dp[n-1];
}
};
|

