4 寻找两个正序数组的中位数

本文最后更新于：2022年4月9日 中午

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

示例 1：

1
2
3
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

1
2
3
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

1
2
输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

1
2
输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

1
2
输入：nums1 = [2], nums2 = []
输出：2.00000

提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

Solution

  • 先将两数组合并，再求中位数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// @lc code=start
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        vector<int> combine;
        int p=0, q=0;
        while(p!=nums1.size() && q!=nums2.size()){
            if(nums1[p]<=nums2[q]){
                combine.push_back(nums1[p++]);
            } else {
                combine.push_back(nums2[q++]);
            }
        }

        while(p!=nums1.size())
            combine.push_back(nums1[p++]);
        while(q!=nums2.size())
            combine.push_back(nums2[q++]);
        
        int n = combine.size();
        double res=0;
        if(n%2==1)
            res = double(combine[n/2]);
        else 
            res = (combine[n/2]+combine[n/2-1])/2.0;
        return res;
    }
};
// @lc code=end
  • 双指针，伪归并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int p=0, q=0;
        int len1 = nums1.size(), len2 = nums2.size();
        int len = len1+len2;
        int mid1=-1, mid2=-1;

        for(int i=0; i<=len/2; ++i){
            mid1 = mid2;
            if(p<len1 && (q>=len2 || nums1[p]<nums2[q]))
                mid2 = nums1[p++];
            else 
                mid2 = nums2[q++];
        }
        if(len%2==1)
            return mid2;
        else 
            return (mid1+mid2)/2.0;
    }
};

参考 LeetCode官方 、geek-8m 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
private:
    int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k){
        int m = nums1.size();
        int n = nums2.size();
        int index1 = 0, index2 = 0;

        while(1){
            if(index1==m)
                return nums2[index2+k-1];
            if(index2==n)
                return nums1[index1+k-1];
            if(k==1)
                return min(nums1[index1], nums2[index2]);

            // 正常情况
            int newIndex1 = min(index1+k/2-1, m-1);
            int newIndex2 = min(index2+k/2-1, n-1);
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            if(pivot1 <= pivot2){
                k-=(newIndex1-index1+1);
                index1 = newIndex1+1;
            } else{
                k-=(newIndex2-index2+1);
                index2 = newIndex2+1;
            }
        }
        return -1;
    }

public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int total = nums1.size()+nums2.size();
        if(total%2==1)
            return getKthElement(nums1, nums2, (total+1)/2);
        else 
            return (getKthElement(nums1, nums2, total/2) 
                    + getKthElement(nums1,nums2,total/2+1)) / 2.0;
    }
};

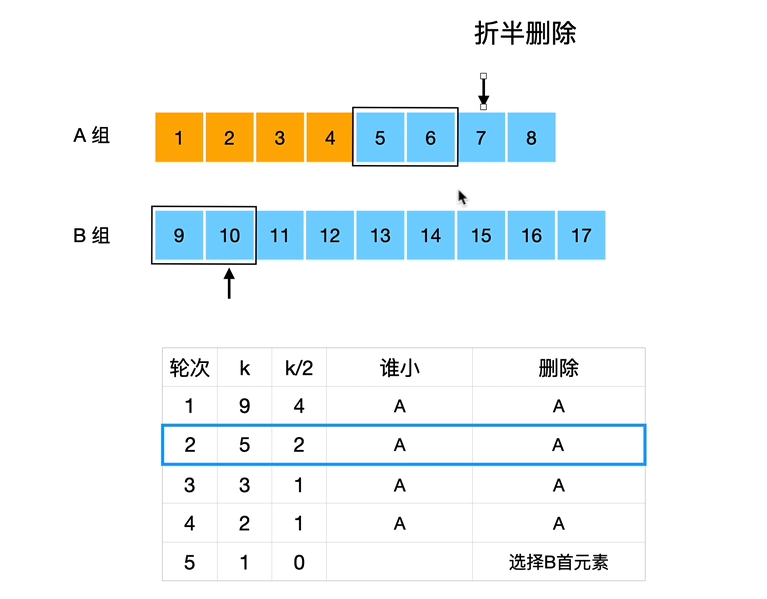
折半删除求第 K 小数

image-20210131162812797

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k){
    int m = nums1.size();
    int n = nums2.size();
    int index1 = 0, index2 = 0;

    while(1){
        if(index1==m)
            return nums2[index2+k-1];
        if(index2==n)
            return nums1[index1+k-1];
        if(k==1)
            return min(nums1[index1], nums2[index2]);

        // 正常情况
        int newIndex1 = min(index1+k/2-1, m-1);
        int newIndex2 = min(index2+k/2-1, n-1);
        int pivot1 = nums1[newIndex1];
        int pivot2 = nums2[newIndex2];
        if(pivot1 <= pivot2){
            k-=(newIndex1-index1+1);
            index1 = newIndex1+1;
        } else{
            k-=(newIndex2-index2+1);
            index2 = newIndex2+1;
        }
    }
    return -1;
}

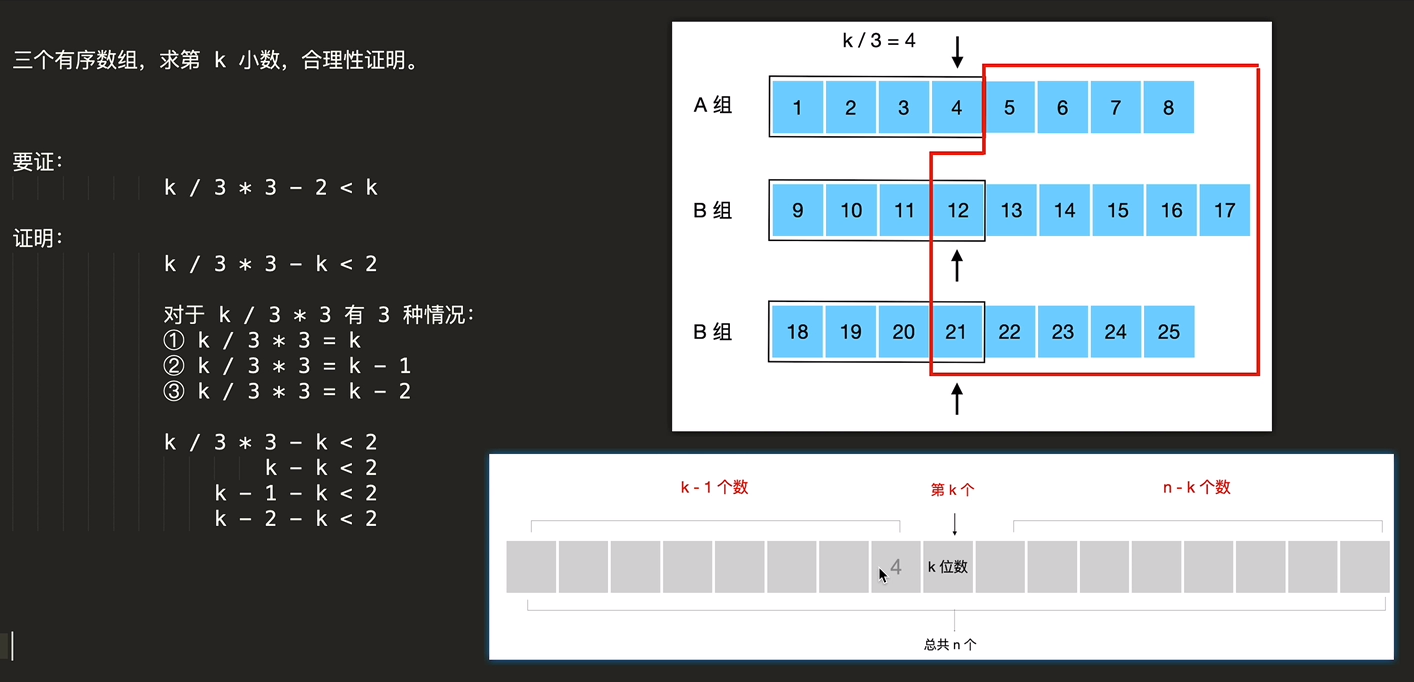
拓展到求 n 组数组中的第 K 小数

image-20210131172010487

algo leetcode 算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！