110 平衡二叉树
本文最后更新于:2022年4月9日 中午
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
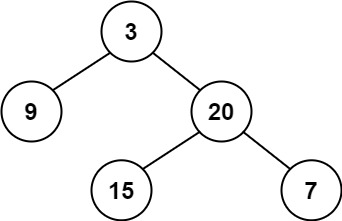
1 | |
示例 2:
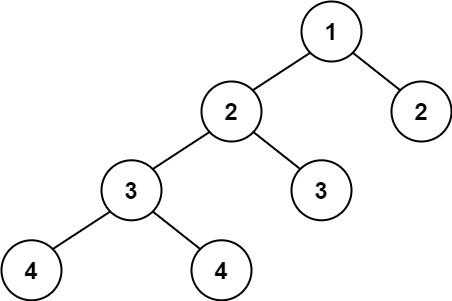
1 | |
示例 3:
1 | |
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
Solution
参考 代码随想录
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
求深度可以从上到下去查,所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)。
根节点的高度就是这颗树的最大深度,所以也可以使用后序遍历。
- 递归法
- 分别求出左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是平衡二叉树了。
1 | |
- 迭代法,见参考链接,了解即可。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!