654 最大二叉树

本文最后更新于：2022年4月9日 中午

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

  1. 二叉树的根是数组 nums 中的最大元素。
  2. 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
  3. 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。

返回有给定数组 nums 构建的 最大二叉树 。

示例 1：

img 
1
2
3
4
5
6
7
8
9
10
11
12
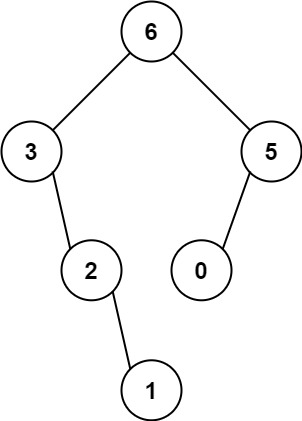
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

img 
1
2
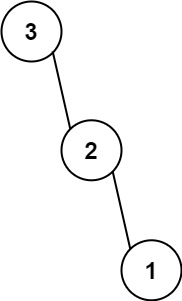
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000
  • nums 中的所有整数 互不相同

Solution

参考 代码随想录

其他相似题型 [106 从中序与后序遍历序列构造二叉树] 、[105 从前序与中序遍历序列构造二叉树]

  • 递归法

  • 确定单层递归的逻辑

    1. 先要找到数组中最大的值和对应的下标， 最大的值构造根节点，下标用来下一步分割数组。

    2. 最大值所在的下标左区间 构造左子树

    3. 最大值所在的下标右区间 构造右子树

「注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下表索引直接在原数组上操作，这样可以节约时间和空间上的开销。」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums, 0, nums.size());
    }
private:
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left >= right) return nullptr;
        // 找到分割点
        int maxValueIndex = left;
        for (int i = left + 1; i < right; ++i) {
            if (nums[i] > nums[maxValueIndex]) {
                maxValueIndex = i;
            }
        }

        TreeNode* root = new TreeNode(nums[maxValueIndex]);
        // 构造左子树，左闭右开
        root->left = traversal(nums, left, maxValueIndex);
        // 构造右子树，左闭右开
        root->right = traversal(nums, maxValueIndex + 1, right);
        return root;
    }
};
// @lc code=end