669 修剪二叉搜索树

本文最后更新于：2022年4月9日 中午

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

img 
1
2
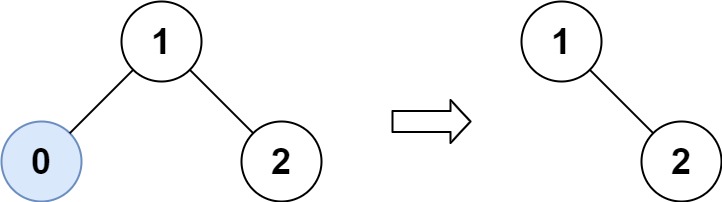
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

img 
1
2
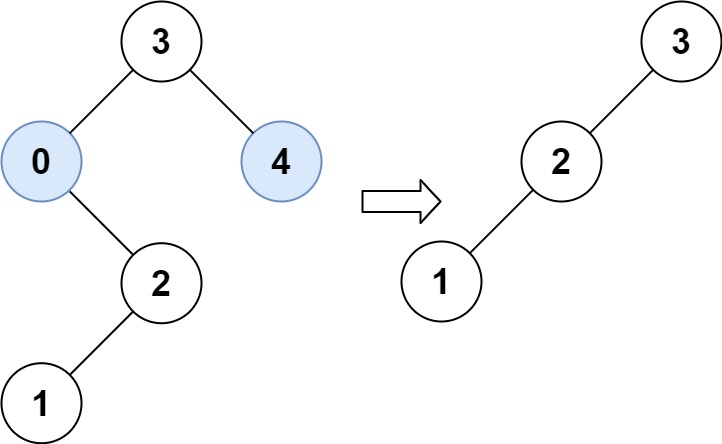
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

示例 3：

1
2
输入：root = [1], low = 1, high = 2
输出：[1]

示例 4：

1
2
输入：root = [1,null,2], low = 1, high = 3
输出：[1,null,2]

示例 5：

1
2
输入：root = [1,null,2], low = 2, high = 4
输出：[2]

提示：

  • 树中节点数在范围 [1, 104] 内
  • 0 <= Node.val <= 104
  • 树中每个节点的值都是唯一的
  • 题目数据保证输入是一棵有效的二叉搜索树
  • 0 <= low <= high <= 104

Solution

参考 代码随想录

  • 递归法
  • 确定递归函数的参数以及返回值
  • 确定终止条件
  • 确定单层递归的逻辑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr) return nullptr;
        if (root->val < low) return trimBST(root->right, low, high);
        if (root->val > high) return trimBST(root->left, low, high);

        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};
// @lc code=end
  • 迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr) return root;
		
        // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while (root && (root->val < low || root->val > high)) {
            if (root->val < low) root = root->right;
            else root = root->left;
        }

        // 此时root已经在[L, R] 范围内，处理左孩子小于L的情况
        TreeNode* cur = root;
        while (cur != nullptr) {
            while (cur->left && cur->left->val < low) {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }

        // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        cur = root;
        while (cur != nullptr) {
            while (cur->right && cur->right->val > high) {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};