给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

1. 给定数组的长度不会超过15。
2. 数组中的整数范围是 [-100,100]。
3. 给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

Solution

参考 代码随想录

• 回溯法
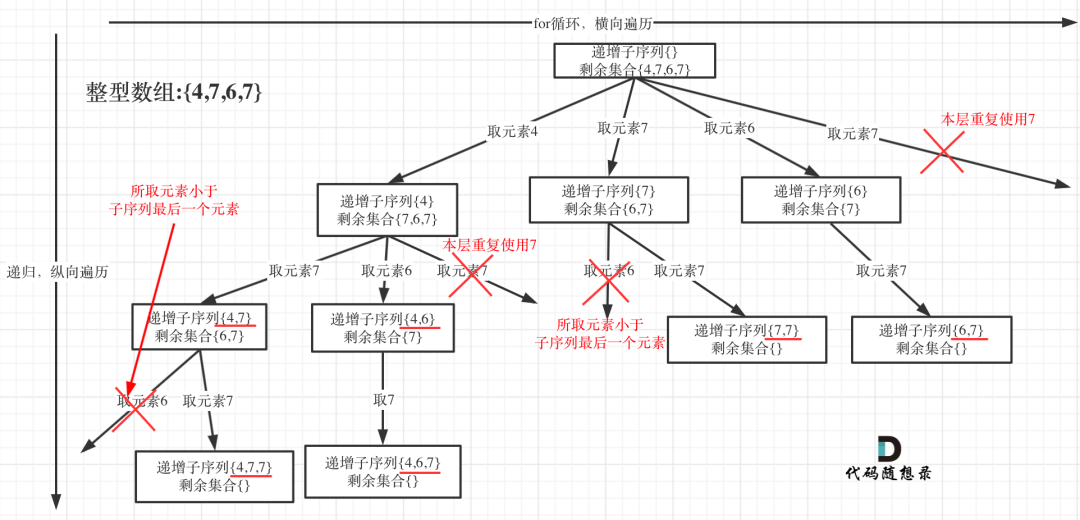
• 本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。
• 同层上使用过的元素就不能在使用了，另外，如果选取的元素小于子序列最后一个元素，那么就不是递增的，所以也要pass掉。
• 使用 used 数组记录本层元素是否重复使用，新的一层 used 都会重新定义（清空），所以要知道 used 只负责本层。

// @lc code=start
class Solution {
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        res.clear();
        vector<int> cur;
        backtrack(nums, 0, cur);
        return res;
    }
private:
    vector<vector<int>> res;

    void backtrack(const vector<int>& nums, int index, vector<int>& cur) {
        if (cur.size() >= 2) {
            res.push_back(cur);
        }
        int used[201] = {0};  // 用来记录本层使用过的元素

        for (int i = index; i < nums.size(); ++i) {
            // 去重，剪枝
            if ((!cur.empty() && nums[i] < cur.back()) || used[nums[i]+100] == 1) {
                continue;
            }
            used[nums[i]+100] = 1;  // 标记本层该元素使用过了
            cur.push_back(nums[i]);
            backtrack(nums, i + 1, cur);
            cur.pop_back();
        }
        return;
    }
};
// @lc code=end

对比 [90 子集 II] 去重差异：（参考 代码随想录1 、代码随想录2 ）

• [491 递增子序列] 去重是同一个父节点下的本层的去重。 used 数组 放在单层搜索逻辑中，而不是放在全局变量。（对比 [46 全排列] ）
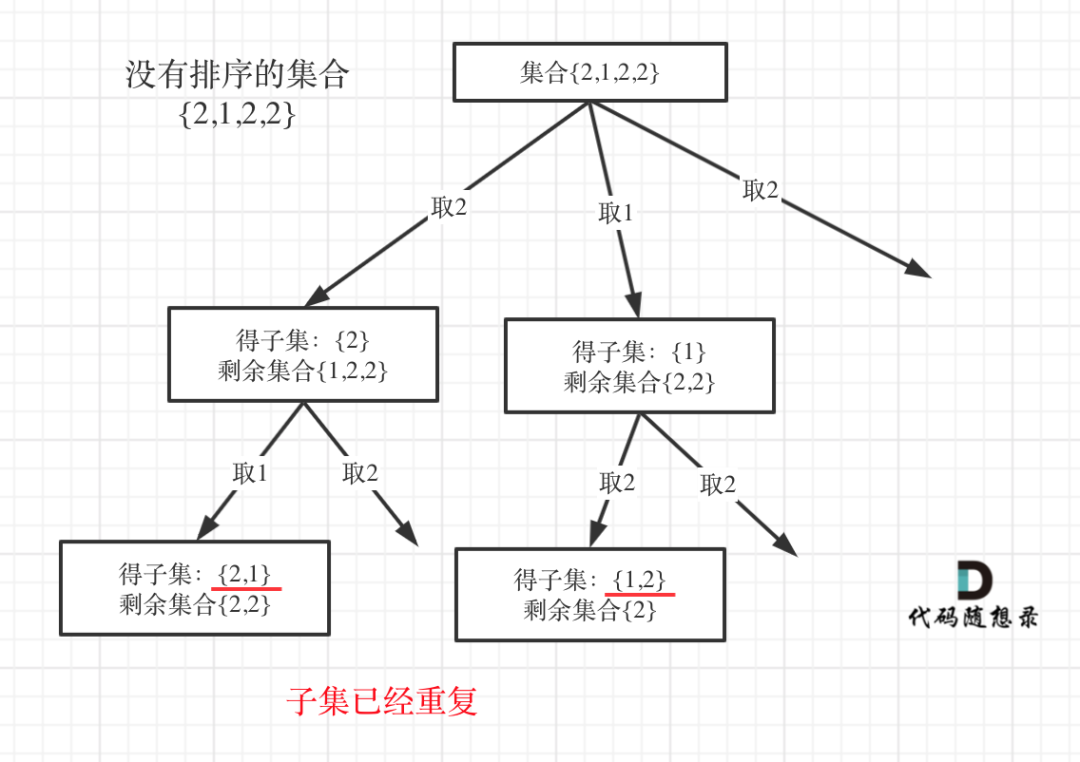
• [90 子集 II] 去重也是同一个父节点下的本层的去重，但子集问题一定要排序，与前一个树枝对比就可以了。

例如：没有排序的集合 {2,1,2,2}