实现 LFU 缓存数据结构。

参考：力扣—460 LFU缓存

• LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
• int get(int key) - 如果键存在于缓存中，则获取键的值，否则返回 -1。
• void put(int key, int value) - 如果键已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最久未使用 的键。

参考题解：@王尼玛

• 两个哈希表 + N个双链表
• key-node 哈希表、freq-LinkedList 哈希表

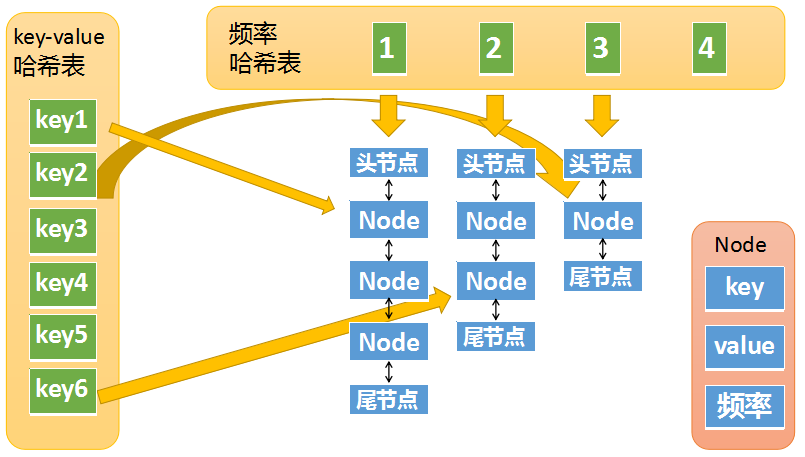
第一个 freq_table 以频率 freq 为索引，每个索引存放一个双向链表，这个链表里存放所有使用频率为 freq 的缓存，缓存里存放三个信息，分别为键 key，值 value，以及使用频率 freq。

第二个 key_table 以键值 key 为索引，每个索引存放对应缓存在 freq_table 中链表里的内存地址，这样我们就能利用两个哈希表来使得两个操作的时间复杂度均为 O(1)。同时需要记录一个当前缓存最少使用的频率 minFreq，这是为了删除操作服务的。

• int get(int key)

对于 get(key) 操作，我们能通过索引 key 在 key_table 中找到缓存在 freq_table 中的链表的内存地址，如果不存在直接返回 -1，否则我们能获取到对应缓存的相关信息，这样我们就能知道缓存的键值还有使用频率，直接返回 key 对应的值即可。

但是我们注意到 get 操作后这个缓存的使用频率加一了，所以我们需要更新缓存在哈希表 freq_table 中的位置。已知这个缓存的键 key，值 value，以及使用频率 freq，那么该缓存应该存放到 freq_table 中 freq + 1 索引下的链表中。

• void put(int key, int value)

对于 put(key, value) 操作，我们先通过索引 key在 key_table 中查看是否有对应的缓存，如果有的话，其实操作等价于 get(key) 操作，唯一的区别就是我们需要将当前的缓存里的值更新为 value。如果没有的话，相当于是新加入的缓存，如果缓存已经到达容量，需要先删除最近最少使用的缓存，再进行插入。

先考虑插入，由于是新插入的，所以缓存的使用频率一定是 1，所以我们将缓存的信息插入到 freq_table 中 1 索引下的列表头即可，同时更新 key_table[key] 的信息，以及更新 minFreq = 1。

考虑删除操作了，由于我们实时维护了 minFreq，所以我们能够知道 freq_table 里目前最少使用频率的索引，同时因为我们保证了链表中从链表头到链表尾的插入时间是有序的，所以 freq_table[minFreq] 的链表中链表尾的节点即为使用频率最小且插入时间最早的节点，我们删除它同时根据情况更新 minFreq ，整个时间复杂度均为 O(1)。

代码看看就好。。。

// 缓存的节点信息
struct Node {
    int key, val, freq;
    Node(int _key,int _val,int _freq): key(_key), val(_val), freq(_freq){}
};
class LFUCache {
    int minfreq, capacity;
    unordered_map<int, list<Node>::iterator> key_table;
    unordered_map<int, list<Node>> freq_table;
public:
    LFUCache(int _capacity) {
        minfreq = 0;
        capacity = _capacity;
        key_table.clear();
        freq_table.clear();
    }
    
    int get(int key) {
        if (capacity == 0) return -1;
        auto it = key_table.find(key);
        if (it == key_table.end()) return -1;
        list<Node>::iterator node = it -> second;
        int val = node -> val, freq = node -> freq;
        freq_table[freq].erase(node);
        // 如果当前链表为空，我们需要在哈希表中删除，且更新minFreq
        if (freq_table[freq].size() == 0) {
            freq_table.erase(freq);
            if (minfreq == freq) minfreq += 1;
        }
        // 插入到 freq + 1 中
        freq_table[freq + 1].push_front(Node(key, val, freq + 1));
        key_table[key] = freq_table[freq + 1].begin();
        return val;
    }
    
    void put(int key, int value) {
        if (capacity == 0) return;
        auto it = key_table.find(key);
        if (it == key_table.end()) {
            // 缓存已满，需要进行删除操作
            if (key_table.size() == capacity) {
                // 通过 minFreq 拿到 freq_table[minFreq] 链表的末尾节点
                auto it2 = freq_table[minfreq].back();
                key_table.erase(it2.key);
                freq_table[minfreq].pop_back();
                if (freq_table[minfreq].size() == 0) {
                    freq_table.erase(minfreq);
                }
            } 
            freq_table[1].push_front(Node(key, value, 1));
            key_table[key] = freq_table[1].begin();
            minfreq = 1;
        } else {
            // 与 get 操作基本一致，除了需要更新缓存的值
            list<Node>::iterator node = it -> second;
            int freq = node -> freq;
            freq_table[freq].erase(node);
            if (freq_table[freq].size() == 0) {
                freq_table.erase(freq);
                if (minfreq == freq) minfreq += 1;
            }
            freq_table[freq + 1].push_front(Node(key, value, freq + 1));
            key_table[key] = freq_table[freq + 1].begin();
        }
    }
};