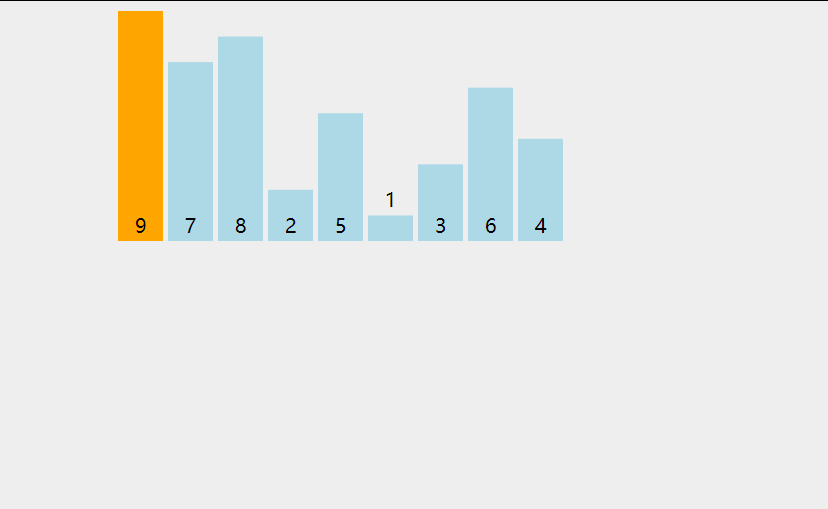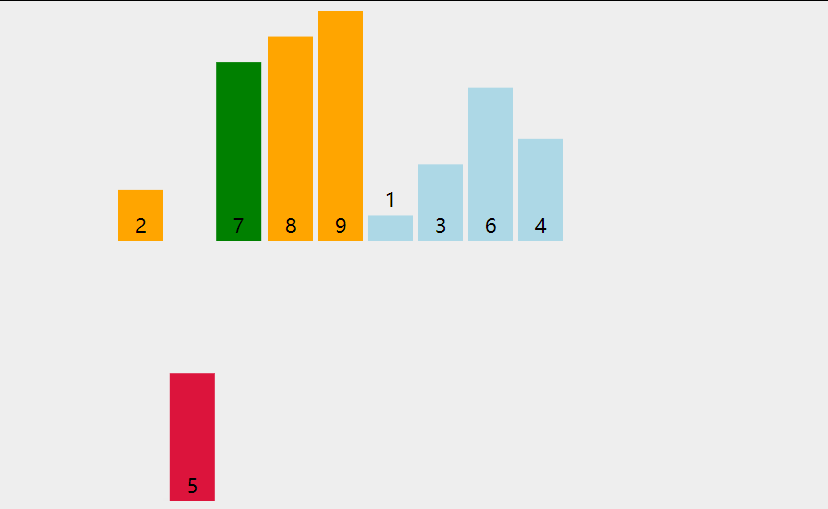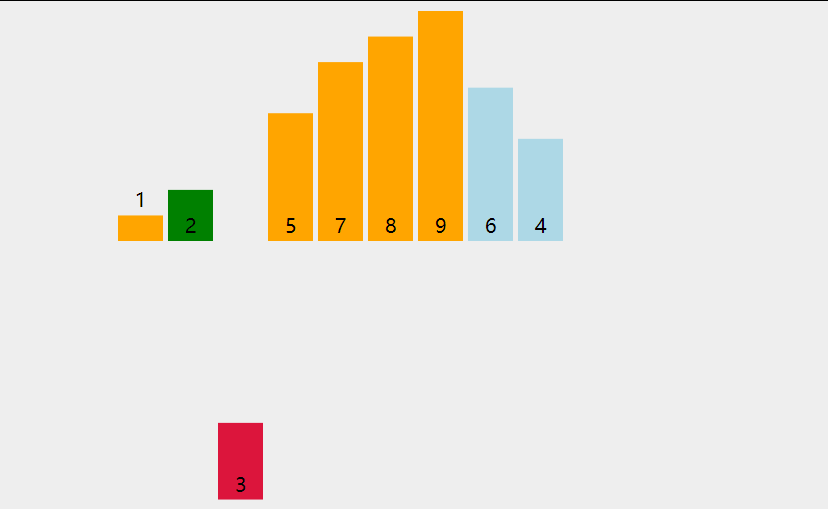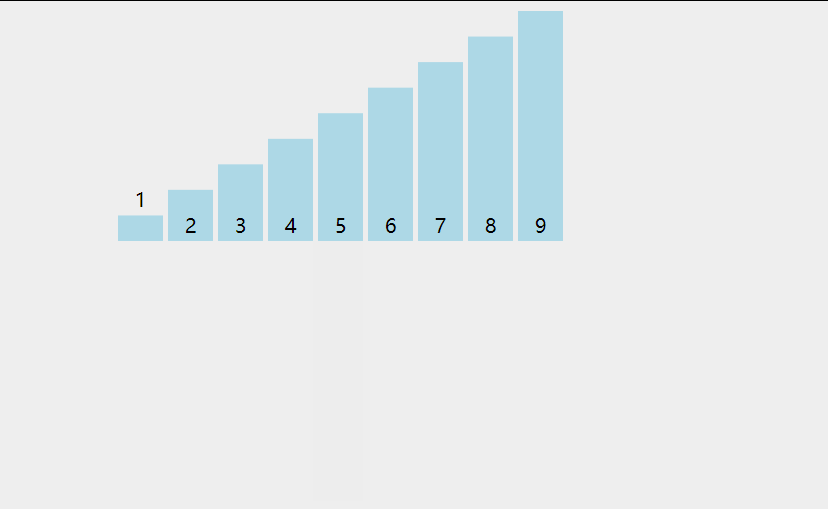常用排序算法

本文最后更新于：2022年4月9日 中午

参考：912. 排序数组

BinarySearch

二分查找（折半查找）：对于已排序，若无序，需要先排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 非递归
int BinarySearch(vector<int> v, int value) {
    if (v.size() <= 0) return -1;
    int low = 0;
    int high = v.size() - 1;
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (v[mid] == value) {
            return mid;
        } else if (v[mid] > value) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return -1;
}

// 递归
int BinarySearch2(vector<int> v, int value, int low, int high) {
    if (low > high) return -1;
    int mid = low + (high - low) / 2;
    if (v[mid] == value) {
        return mid;
    } else if (v[mid] > value) {
        return BinarySearch2(v, value, low, mid-1);
    } else {
        return BinarySearch2(v, value, mid+1, high);
    }
}

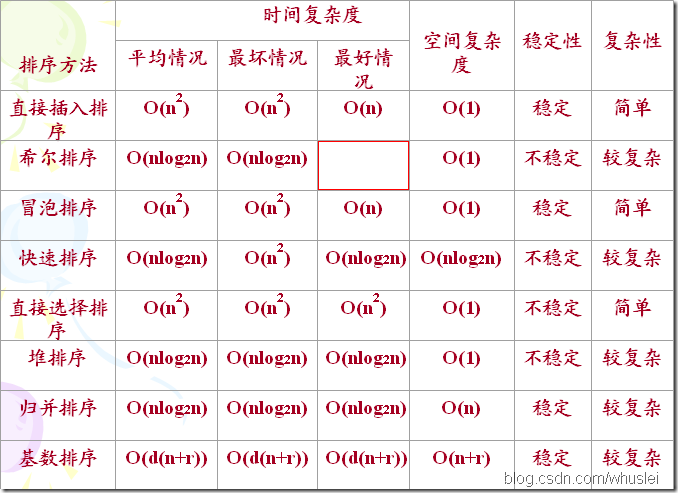
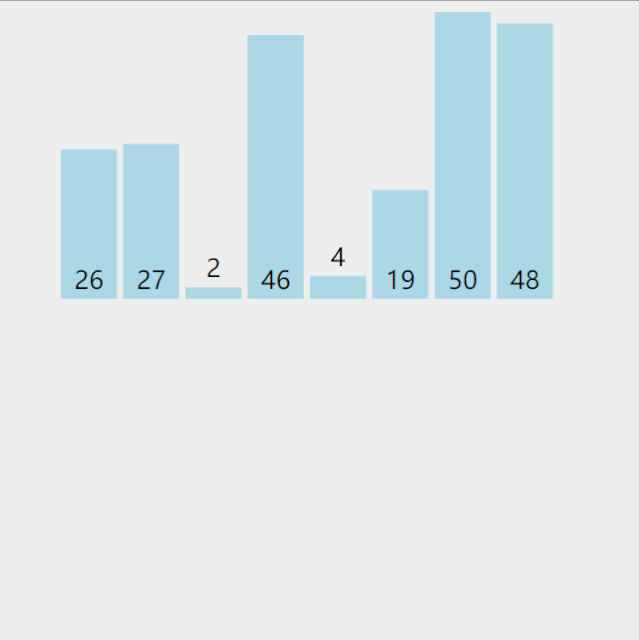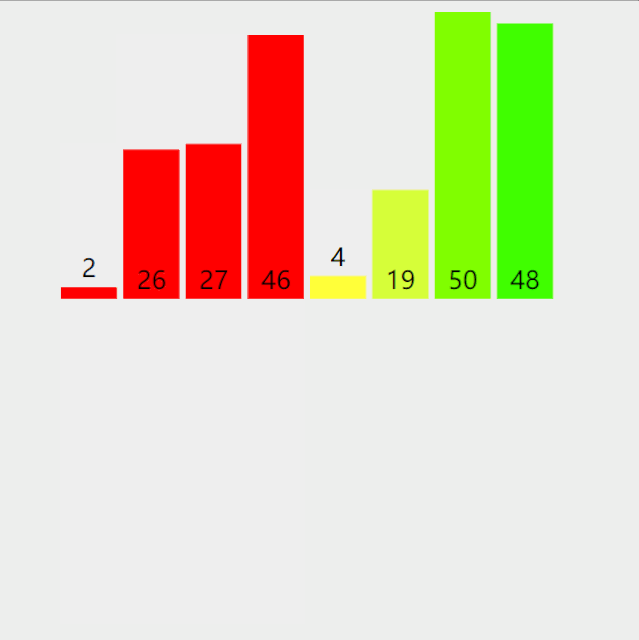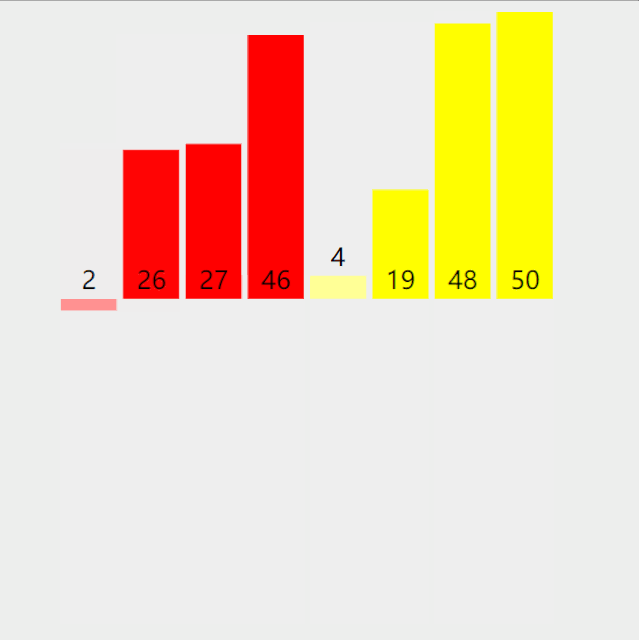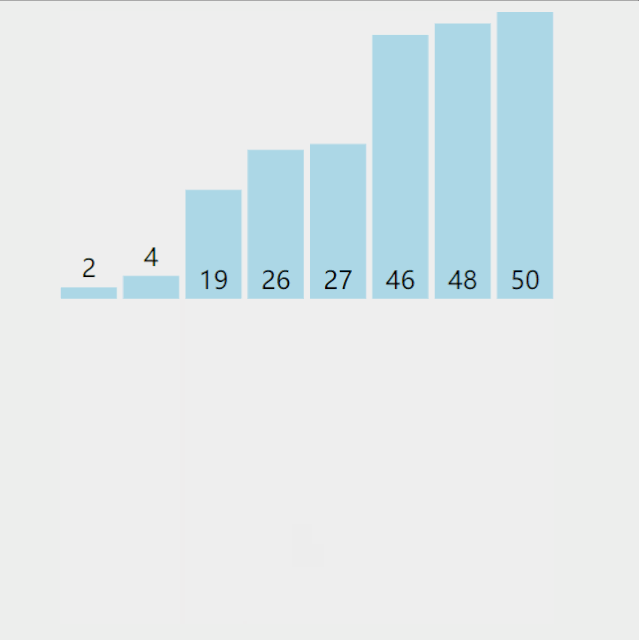
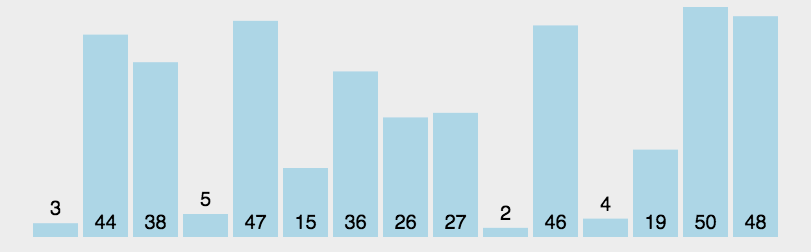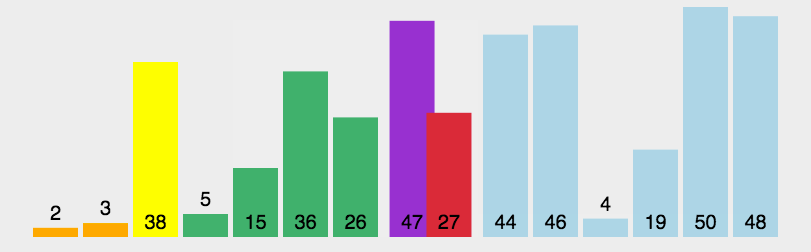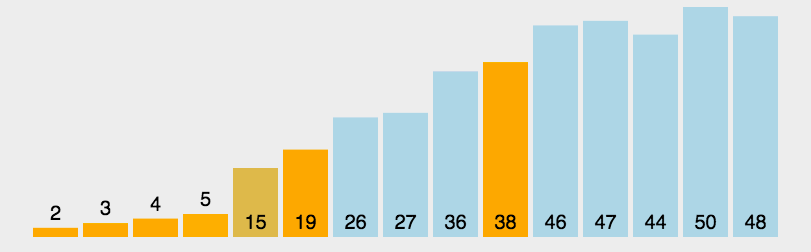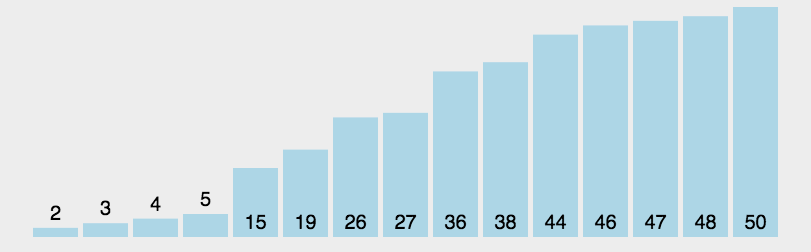
排序算法性能比较

这里写图片描述

BubbleSort

（无序区，有序区）。从无序区通过交换找出最大元素放到有序区前端。

img

排序思路：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的 元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void BubbleSort(vector<int>& v) {
    int len = v.size();
    for (int i = 0; i < len-1; ++i) {
        for (int j = 0; j < len - 1 - i; ++j) {
            if (v[j] > v[j+1]) {
                swap(v[j], v[j+1]);
            }
        }
    }
}

// 改进，借助 swap_check 早停
void BubbleSort2(vector<int>& v) {
    int len = v.size();
    bool swap_check = true;
    for (int i = 0; i < len-1 && swap_check; ++i) {
        swap_check = false;
        for (int j = 0; j < len - 1 - i; ++j) {
            if (v[j] > v[j+1]) {
                swap_check = true;  // 本轮是否发生过交换
                swap(v[j], v[j+1]);
            }
        }
    }
}

优化1（优化外层循环）：

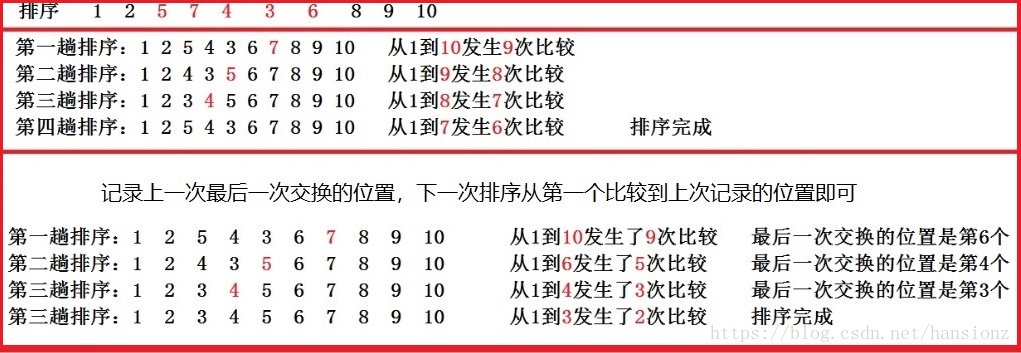
若在某一趟排序中未发现气泡位置的交换，则说明待排序的无序区中所有气泡均满足轻者在上，重者在下的原则，因此，冒泡排序过程可在此趟排序后终止。

优化2（优化内层循环）：记住最后一次交换发生位置lastExchange的冒泡排序

在每趟扫描中，记住最后一次交换发生的位置lastExchange，（该位置之后的相邻记录均已有序）。下一趟排序开始时，R[1..lastExchange-1]是无序区，R[lastExchange..n]是有序区。这样，一趟排序可能使当前无序区扩充多个记录，因此记住最后一次交换发生的位置lastExchange，从而减少排序的趟数。

这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void BubbleSort(int arr[], int len)
{
	int i = 0;
	int tmp = 0;
	int flag = 0;
	int pos = 0;//用来记录最后一次交换的位置
	int k = len - 1;
	for (i = 0; i < len - 1; i++)//确定排序趟数
	{
		pos = 0;
		int j = 0;
		flag = 0;
		for (j = 0; j < k; j++)//确定比较次数
		{
			if (arr[j]>arr[j + 1])
			{
				//交换
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
				flag = 1;//加入标记
				pos = j;//交换元素，记录最后一次交换的位置
			}
		}
		if (flag == 0)//如果没有交换过元素，则已经有序
		{
			return;
		}
		k = pos;//下一次比较到记录位置即可
	}
}

优化三：

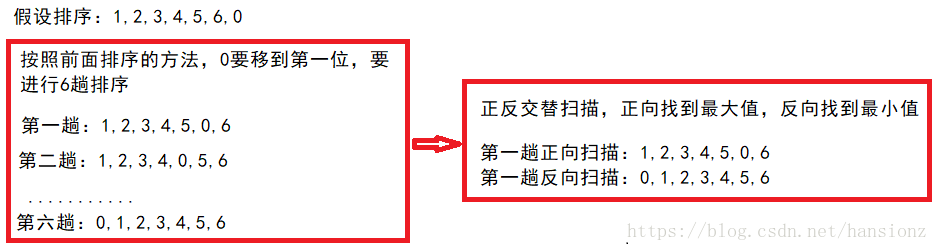
一次排序可以确定两个值，正向扫描找到最大值交换到最后，反向扫描找到最小值交换到最前面。

这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void BubbleSort(int arr[], int len)
{
	int i = 0;
	int j = 0;
	int n = 0;//同时找最大值的最小需要两个下标遍历
	int flag = 0;
	int pos = 0;//用来记录最后一次交换的位置
	int k = len - 1;
	for (i = 0; i < len - 1; i++)//确定排序趟数
	{
		pos = 0;
		flag = 0;
		//正向寻找最大值
		for (j = n; j < k; j++)//确定比较次数
		{
			if (arr[j]>arr[j + 1])
			{
				//交换
				int tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
				flag = 1;//加入标记
				pos = j;//交换元素，记录最后一次交换的位置
			}
		}
		if (flag == 0)//如果没有交换过元素，则已经有序,直接结束
		{
			return;
		}
		k = pos;//下一次比较到记录位置即可
        
        flag = 0;
		//反向寻找最小值
		for (j = k; j > n; j--)
		{
			if (arr[j-1] > arr[j]){
                int tmp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = tmp;
                flag = 1;
            }
		}
		n++;
		if (flag == 0)//如果没有交换过元素，则已经有序,直接结束
		{
			return;
		}
	}
}

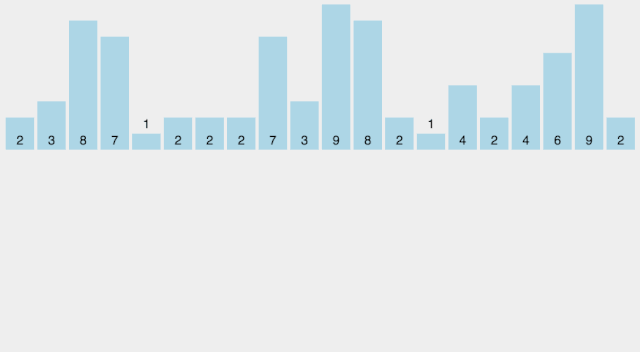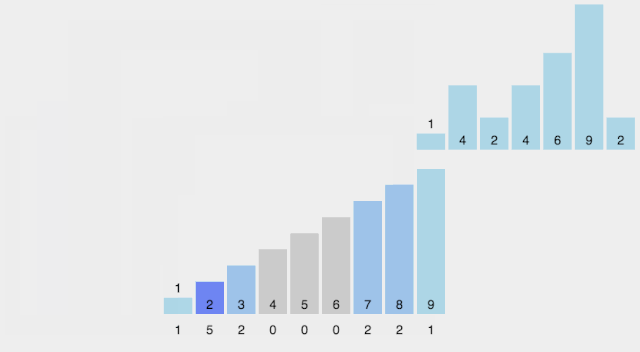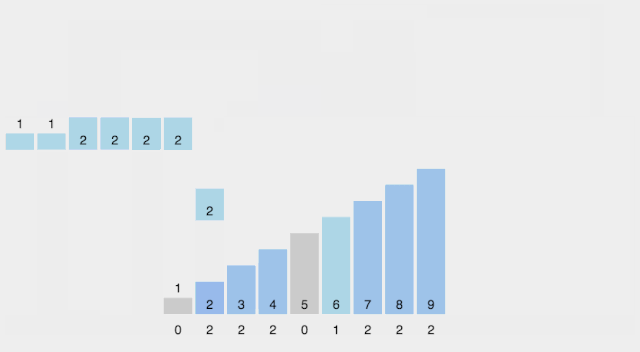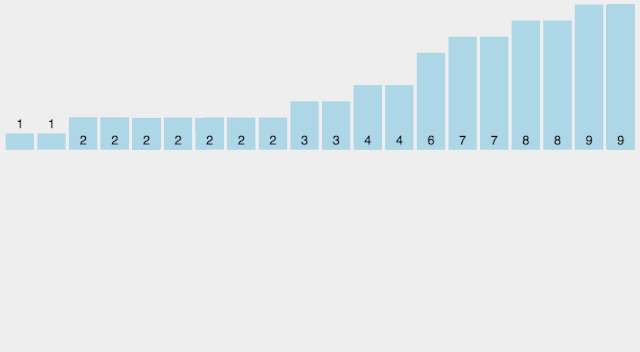
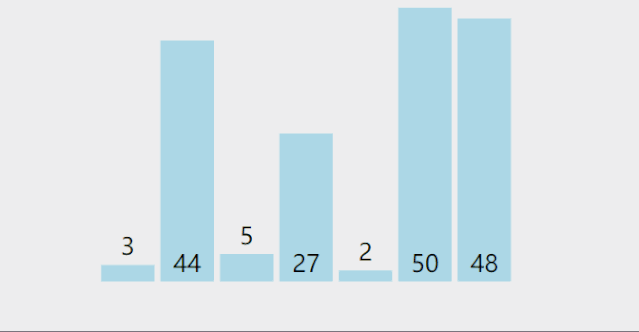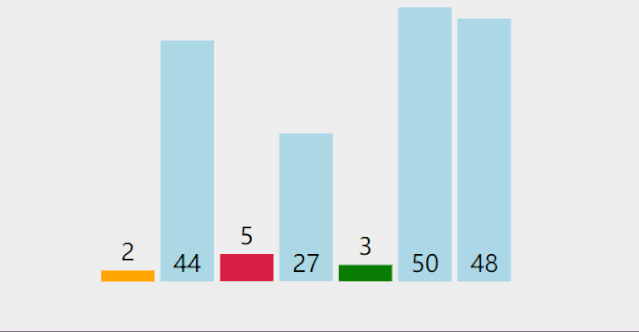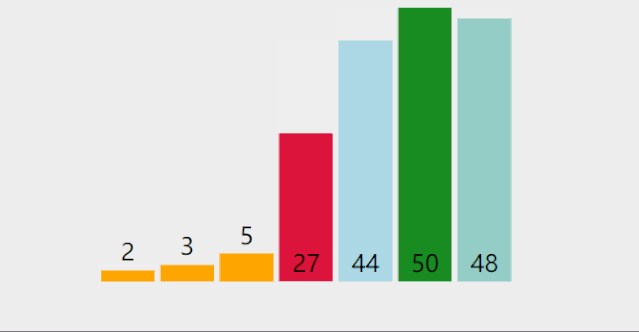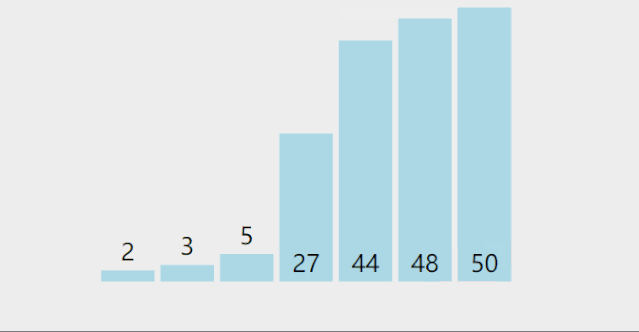
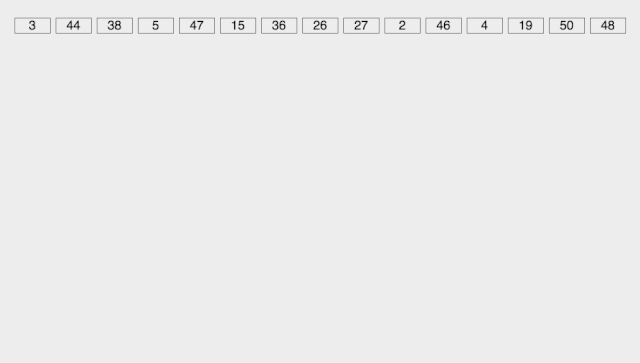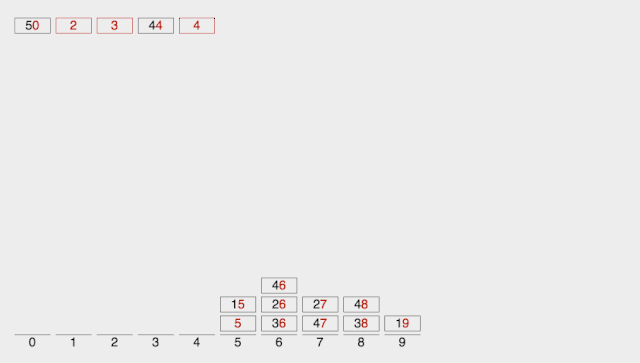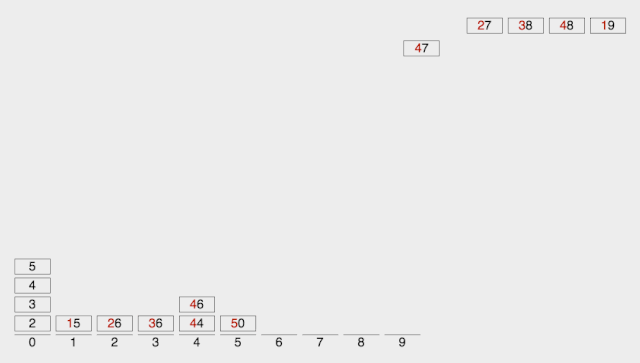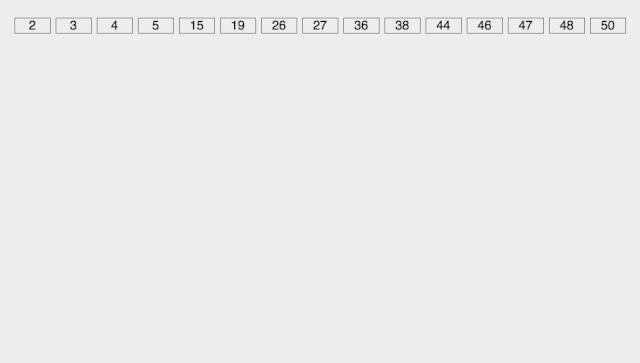
CountSort

计数排序：统计小于等于该元素值的元素的个数 i，于是该元素就放在目标数组的索引 i 位 （i≥0）。

计数排序基于一个假设，待排序数列的所有数均为整数，且出现在（0，k）的区间之内。 如果 k（待排数组的最大值） 过大则会引起较大的空间复杂度，一般是用来排序 0 到 100 之间的数字的最好的算法，但是它不适合按字母顺序排序人名。 计数排序不是比较排序，排序的速度快于任何比较排序算法。 时间复杂度为 O（n+k），空间复杂度为 O（n+k）

计数排序

算法的步骤如下：

  1. 找出待排序的数组中最大和最小的元素
  2. 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项
  3. 对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）
  4. 反向填充目标数组：将每个元素 i 放在新数组的第 C[i] 项，每放一个元素就将 C[i] 减去 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<int> CountSort(vector<int>& v) {
    int minV  = v[0];
    int maxV = v[0];
    for (int i = 0; i < v.size(); ++i) {
        minV = min(minV, v[i]);
        maxV = max(maxV, v[i]);
    }
    vector<int> Count(maxV - minV + 1, 0);

    // 统计每一个键值出现的次数
    for (int i = 0; i < v.size(); ++i) {
        Count[v[i] - minV]++;
    }
	// 后面的键值出现的位置为前面所有键值出现的次数之和
    for (int i = 1; i < Count.size(); ++i) {
        Count[i] += Count[i-1];
    }

    vector<int> Sorted_v(v.size());
    for (int i = v.size()-1; i >= 0; --i) {
        Sorted_v[Count[v[i] - minV] - 1] = v[i];
        Count[v[i] - minV]--;
    }
    return Sorted_v;
}

HeapSort

堆排序：（最大堆，有序区）。从堆顶把根卸出来放在有序区之前，再恢复堆。

参考：https://www.bilibili.com/video/BV1Eb41147dK?from=search&seid=3993837508839965022

https://www.cnblogs.com/wanglei5205/p/8733524.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 非递归
void max_heapify2(int arr[], int n, int i) {
    while (2 * i + 1 < n) {
        int j = 2 * i + 1;
        if (j+1 < n && arr[j+1] > arr[j])   // 比较左右子节点哪个大
            j += 1;

        if (arr[i] >= arr[j])
            break;

        swap(arr[i], arr[j]);
        i = j;  // 向下 heapify
    }
}

// 递归
void max_heapify(int arr[], int n, int i) {
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;

    if (l < n && arr[l] > arr[largest])
        largest = l;

    if (r < n && arr[r] > arr[largest])
        largest = r;

    if (largest != i) {
        swap(arr[i], arr[largest]);
        max_heapify(arr, n, largest);
    }
}

void heapSort(int arr[], int n) {
    // 初始化堆，i 从最后一个父节点开始调整
    for (int i = (n-1)/2; i >= 0; --i)
        max_heapify(arr, n, i);

    // 先将第一个元素和已经排好序的元素前一位交换，再重新调整，取出元素过程
    for (int i = n - 1; i > 0; --i) {
        swap(arr[0], arr[i]);
        max_heapify(arr, i, 0);
    }
}

InsertSort

（有序区，无序区）。把无序区的第一个元素插入到有序区的合适的位置。对数组：比较得 少，换得多。

img

插入排序思路：

  1. 从第一个元素开始，该元素可以认为已经被排序
  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
  4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤 2~5
1
2
3
4
5
6
7
8
9
10
11
12
13
void InsertSort(vector<int>& v) {
    int n = v.size();
    for (int i = 1; i < n; ++i) {
        int tmp = v[i];
        for (int j = i-1; j >= 0; --j) {
            if (v[j] > tmp) {
                v[j+1] = v[j];
                v[j] = tmp;
            } else
                break;
        }
    }
}

MergeSort

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

img

归并排序：把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。可从上到 下或从下到上进行。

  1. 把长度为n的输入序列分成两个长度为n/2的子序列；

  2. 对这两个子序列分别采用归并排序；

  3. 将两个排序好的子序列合并成一个最终的排序序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
void merge(vector<int>& nums, int l, int mid, int r) {
    vector<int>& tmp(nums.size());
    int mid = l + (r - l) / 2;
    // merge 过程
    int i = l, j = mid + 1, pos = l;
    while (i <= mid && j <= r) {
        if (nums[i] < nums[j])
            tmp[pos++] = nums[i++];
        else
            tmp[pos++] = nums[j++];
    }
    while (i <= mid)
        tmp[pos++] = nums[i++];
    while (j <= r) 
        tmp[pos++] = nums[j++];
    // 将合并后的区间赋值给 nums
    for (int index = l; index <= r; ++index)
        nums[index] = tmp[index];
}

// 迭代版
void mergeSort(int arr[], int n) {
    for (int seg = 1; seg < n; seg += seg) {
        for (int i = 0; i < n-seg; i += seg + seg) {
            // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
            if (arr[i+seg-1] > arr[i+seg])  // 优化1
                merge(arr, i, i+seg-1, min(i+seg+seg-1, n-1));
        }
    }
}


// 递归版
void mergeSort2(int arr[], int l, int r) {
    if (l >= r) return;

    int mid = (l + r) / 2;
    mergeSort2(arr, l, mid);
    mergeSort2(arr, mid+1, r);
    // 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
    if (arr[mid] > arr[mid+1])  
        merge(arr, l, mid, r);
}

QuickSort

（小数，基准元素，大数）。在区间中随机挑选一个元素作基准，将小于基准的元素放在基准 之前，大于基准的元素放在基准之后，再分别对小数区与大数区进行排序。

img

快速排序思路：

  1. 选取第一个数为基准，优化1：避免数组有序时，退化为 O(n^2)
  2. 将比基准小的数交换到前面，比基准大的数交换到后面
  3. 对左右区间重复第二步，直到各区间只有一个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void quickSort(vector<int>& v, int low, int high) {
    if (low >= high) return;

    swap(v[low], v[rand()%(high-low+1) + low]); // 优化1
    int pivot = v[low];

    int p = low;
    for (int i = low+1; i <= high; ++i) {
        if (v[i] < pivot) {
            p++;
            swap(v[p], v[i]);
        }
    }
    swap(v[low], v[p]);

    quickSort(v, low, p-1);
    quickSort(v, p+1, high);
}

双路快排

http://coding.imooc.com/learn/questiondetail/4920.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// 双路快速排序的partition
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
template <typename T>
int _partition2(T arr[], int l, int r){

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l] , arr[rand()%(r-l+1)+l] );
    T v = arr[l];

    // arr[l+1...i) <= v; arr(j...r] >= v
    int i = l+1, j = r;
    while( true ){
        // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
        // 思考一下为什么?
        while( i <= r && arr[i] < v )
            i ++;

        // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
        // 思考一下为什么?
        while( j >= l+1 && arr[j] > v )
            j --;
		
        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        i ++;
        j --;
    }

    swap( arr[l] , arr[j]);

    return j;
}

// 对arr[l...r]部分进行快速排序
template <typename T>
void _quickSort(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 调用双路快速排序的partition
    int p = _partition2(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

三路快排

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void __quickSort3Ways(T arr[], int l, int r){

    // 对于小规模数组, 使用插入排序进行优化
    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
    swap( arr[l], arr[rand()%(r-l+1)+l ] );

    T v = arr[l];

    int lt = l;     // arr[l+1...lt] < v
    int gt = r + 1; // arr[gt...r] > v
    int i = l+1;    // arr[lt+1...i) == v
    while( i < gt ){
        if( arr[i] < v ){
            swap( arr[i], arr[lt+1]);
            i ++;
            lt ++;
        }
        else if( arr[i] > v ){
            swap( arr[i], arr[gt-1]);
            gt --;
        }
        else{ // arr[i] == v
            i ++;
        }
    }

    swap( arr[l] , arr[lt] );

    __quickSort3Ways(arr, l, lt-1);
    __quickSort3Ways(arr, gt, r);
}

SelectionSort

（有序区，无序区）。在无序区里找一个最小的元素跟在有序区的后面。对数组：比较得多， 换得少。

选择排序

选择排序思路：

  1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  2. 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
  3. 以此类推，直到所有元素均排序完毕
  4. 时间负复杂度：O(n^2)，空间O(1)，非稳定排序，原地排序
1
2
3
4
5
6
7
8
9
10
11
12
void selectSort(vector<int>& v) {
    int minIndex, n = v.size();
    for (int i = 0; i < n; ++i) {
        minIndex = i;
        for (int j = i + 1; j < n; ++j) {
            if (v[j] < v[minIndex]) {
                minIndex = j;
            }
        }
        swap(v[i], v[minIndex]);
    }
}

ShellSort

希尔排序：每一轮按照事先决定的间隔进行插入排序，间隔会依次缩小，最后一次一定要 是 1。

希尔排序就是为了加快速度简单地改进了插入排序，交换不相邻的元素以对数组的局部进行排序。

参考：https://mp.weixin.qq.com/s/4kJdzLB7qO1sES2FEW0Low

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void shellSort(vector<int>& v) {
    int n = v.size();
    int h = 1;
    while (h < n/3) {
        h = 3*h + 1;
    }

    while (h >= 1) {
        for (int i = h; i < n; ++i) {
            //从第gap个元素，逐个对其所在组进行直接插入排序操作
            for (int j = i; j >= h && v[j] < v[j-h]; j -= h) {
                swap(v[j], v[j-h]);
            }
        }
        h = h / 3;
    }
}

BucketSort

桶排序：将值为 i 的元素放入 i 号桶，最后依次把桶里的元素倒出来。

桶排序

桶排序序思路：

  1. 设置一个定量的数组当作空桶子。
  2. 寻访序列，并且把项目一个一个放到对应的桶子去。
  3. 对每个不是空的桶子进行排序。
  4. 从不是空的桶子里把项目再放回原来的序列中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void BucketSort(vector<int>& v) {
    int n = v.size();
    vector<int>* bucket =new vector<int>(n, 0);

    for (int i = 0; i < n; ++i) {
        int index = v[i] / n;
        bucket[index].push_back(v[i]);
    }

    for (int i = 0; i < n; ++i) {
        sort(bucket[i].begin(), bucket[i].end());
    }

    int index = 0;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < bucket[i].size(); ++j) {
            v[index++] = bucket[i][j];
        }
    }
    delete [] bucket;
}

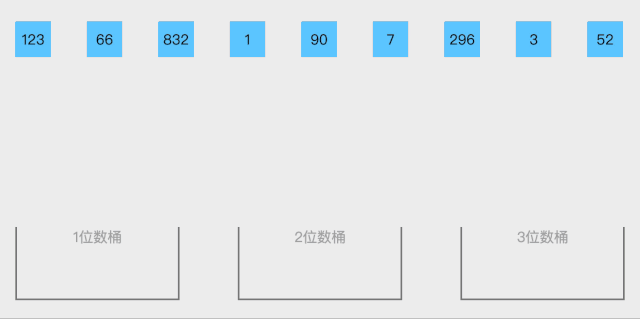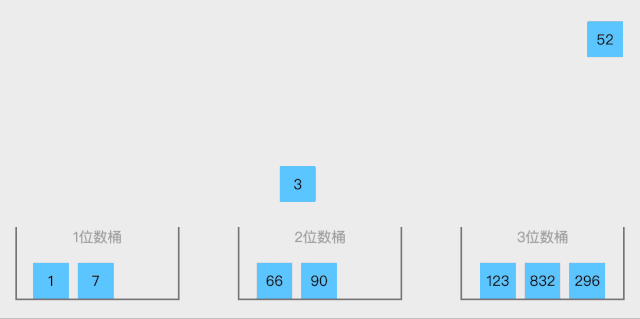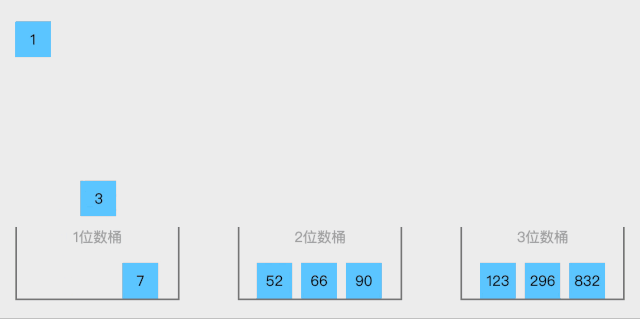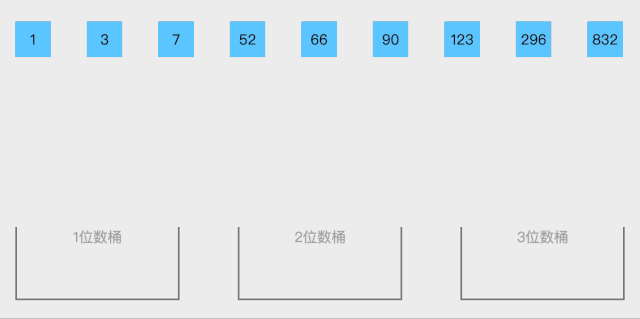
BaseSort

一种多关键字的排序算法，可用桶排序实现。

基数排序

算法思想：

  1. 取得数组中的最大数，并取得位数；
  2. arr为原始数组，从最低位开始取每个位组成radix数组；
  3. 对radix进行计数排序（利用计数排序适用于小范围数的特点）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
int maxbit(int data[], int n) //辅助函数，求数据的最大位数
{
    int maxData = data[0];		///< 最大数
    /// 先求出最大数，再求其位数，这样有原先依次每个数判断其位数，稍微优化点。
    for (int i = 1; i < n; ++i)
    {
        if (maxData < data[i])
            maxData = data[i];
    }
    int d = 1;
    int p = 10;
    while (maxData >= p)
    {
        //p *= 10; // Maybe overflow
        maxData /= 10;
        ++d;
    }
    return d;
/*    int d = 1; //保存最大的位数
    int p = 10;
    for(int i = 0; i < n; ++i)
    {
        while(data[i] >= p)
        {
            p *= 10;
            ++d;
        }
    }
    return d;*/
}
void radixsort(int data[], int n) //基数排序
{
    int d = maxbit(data, n);
    int *tmp = new int[n];
    int *count = new int[10]; //计数器
    int i, j, k;
    int radix = 1;
    for(i = 1; i <= d; i++) //进行d次排序
    {
        for(j = 0; j < 10; j++)
            count[j] = 0; //每次分配前清空计数器
        for(j = 0; j < n; j++)
        {
            k = (data[j] / radix) % 10; //统计每个桶中的记录数
            count[k]++;
        }
        for(j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
        for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
        {
            k = (data[j] / radix) % 10;
            tmp[count[k] - 1] = data[j];
            count[k]--;
        }
        for(j = 0; j < n; j++) //将临时数组的内容复制到data中
            data[j] = tmp[j];
        radix = radix * 10;
    }
    delete []tmp;
    delete []count;
}

参考资料：

https://github.com/forthespada/InterviewGuide/blob/main/Doc/Knowledge/%E7%AE%97%E6%B3%95/%E7%AE%97%E6%B3%95%E5%9F%BA%E7%A1%80/%E5%8D%81%E5%A4%A7%E6%8E%92%E5%BA%8F.md

https://mp.weixin.qq.com/s/ekGdneZrMa23ALxt5mvKpQ

https://www.cnblogs.com/onepixel/p/7674659.html

https://visualgo.net/zh/sorting?slide=10-2

algo 排序算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！