114 二叉树展开为链表

本文最后更新于：2022年4月9日 中午

给你二叉树的根结点 root ，请你将它展开为一个单链表：

  • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
  • 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

img

1
2
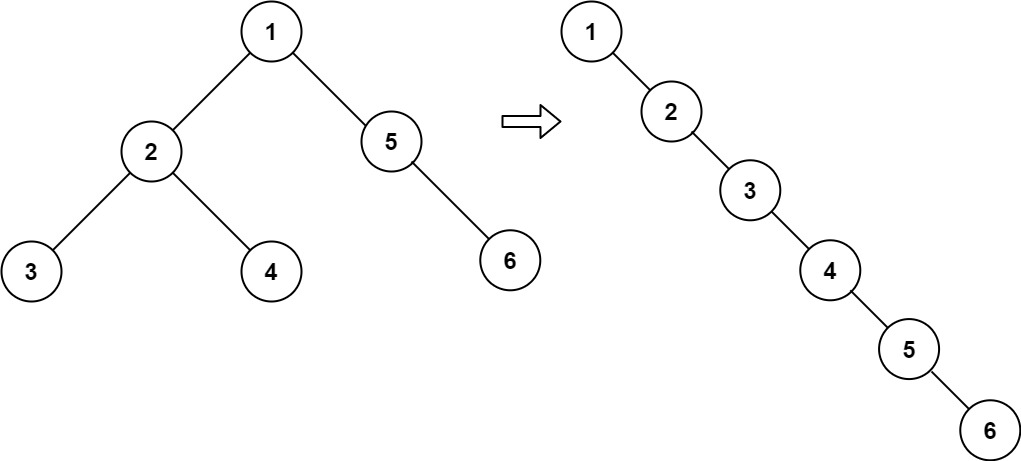
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

1
2
输入：root = []
输出：[]

示例 3：

1
2
输入：root = [0]
输出：[0]

提示：

  • 树中结点数在范围 [0, 2000] 内
  • -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

Solution

参考：LeetCode官方

  • 原地调整，寻找前驱结点
  • 具体做法是，对于当前节点，如果其左子节点不为空，则在其左子树中找到最右边的节点，作为前驱节点，将当前节点的右子节点赋给前驱节点的右子节点，然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// @lc code=start
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if (root == nullptr) return;
        TreeNode* cur = root;
        while (cur) {
            if (cur->left) {
                TreeNode* nex = cur->right;
                TreeNode* pre = cur->left;
                while (pre->right) pre = pre->right;
                pre->right = nex;
                cur->right = cur->left;
                cur->left = nullptr;
            }
            cur = cur->right;
        }
    }
};
// @lc code=end
  • 前序遍历，借助vector容器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    void flatten(TreeNode* root) {
        vector<TreeNode*> l;
        preorderTraversal(root, l);
        int n = l.size();
        for (int i = 1; i < n; i++) {
            TreeNode *prev = l.at(i - 1), *curr = l.at(i);
            prev->left = nullptr;
            prev->right = curr;
        }
    }

    void preorderTraversal(TreeNode* root, vector<TreeNode*> &l) {
        if (root != NULL) {
            l.push_back(root);
            preorderTraversal(root->left, l);
            preorderTraversal(root->right, l);
        }
    }
};
algo leetcode 二叉树

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！