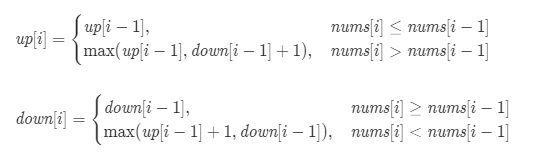本文最后更新于:2022年4月9日 中午
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
| 输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。
|
示例 2:
| 输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
|
示例 3:
| 输入: [1,2,3,4,5,6,7,8,9]
输出: 2
|
进阶:
你能否用 O(n) 时间复杂度完成此题?
Solution
参考 liuyubobobo 、lgh18
动态规划
- 借助 dp 数组
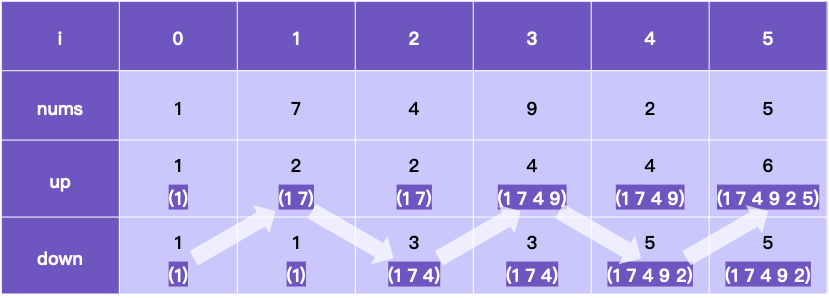
- 假设 up[i] 表示 nums[0:i] 中最后两个数字递增的最长摆动序列长度,down[i] 表示 nums[0:i] 中最后两个数字递减的最长摆动序列长度,只有一个数字时默认为 1。
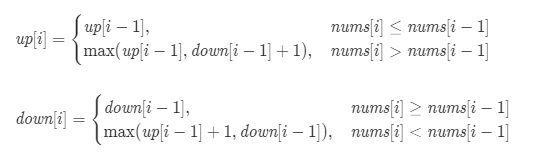
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if(n<2)
return n;
vector<int> up(n,1), down(n,1);
for(int i=1; i<n; ++i){
if(nums[i]>nums[i-1]){
up[i] = max(up[i-1], down[i-1]+1);
down[i] = down[i-1];
} else if(nums[i]<nums[i-1]){
up[i] = up[i-1];
down[i] = max(down[i-1], up[i-1]+1);
} else {
up[i] = up[i-1];
down[i] = down[i-1];
}
}
return max(up[n-1], down[n-1]);
}
};
|
| class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size()<=1) return nums.size();
int up=1, down=1;
for(int i=1; i<nums.size(); ++i){
if(nums[i]>nums[i-1])
up = max(up, down+1);
else if(nums[i]<nums[i-1])
down = max(down, up+1);
}
return max(up, down);
}
};
|
参考 代码随想录
贪心算法
- 我们只需要统计该序列中「峰」与「谷」的数量即可(注意序列两端的数也是「峰」或「谷」),但需要注意处理相邻的相同元素。
- 实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if (n < 2) return n;
int preDiff = 0;
int curDiff = 0;
int res = 1;
for (int i = 1; i < n; ++i) {
curDiff = nums[i] - nums[i-1];
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
res++;
preDiff = curDiff;
}
}
return res;
}
};
|