实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

Solution

参考 @leetcode官方

注意变形要求小数点精确到xxx

• 暴力法

class Solution {
public:
    int mySqrt(int x) {
        int res = 0;
        for (int i = 0; (long long)i*i <= x; ++i) {
            res = max(res, i);
        }
        return res;
    }
};

• 二分查找

• 如果一个数 a 的平方大于 x ，那么 a 一定不是 x 的平方根。我们下一轮需要在 [0..a - 1] 区间里继续查找 x 的平方根。

• r 一定会停在 mid*mid <= x 的最大那个mid的位置，因为 mid*mid=x 的mid如果存在的话在上面就已经返回了，所以这里只需要返回r就好了

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid < x) {
                l = mid + 1;
            } else if ((long long)mid * mid > x) {
                r = mid - 1;
            } else {
                return mid;
            }
        }
        return r;
    }
};

• 牛顿法

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (fabs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return int(x0);
    }
};

拓展：

参考：用二分法和牛顿迭代法求一个正数的平方根

二分法

这里的题目稍微宽了一点点，包含了整数和小数的情况，如果中间值的平方与目标值在误差范围内，则返回，否则根据大小情况改变左/右区间的端点。

#include<iostream>
using namespace std;
int main()
{
    double eps = 1e-6;
    double k = 0.8;  // 输入正数
    double l = 0.0,r,mid;
    if (k>=1) r = k;  // 若输入正数大于1，则右端点设为 k
    if (k<1)  r = 1;  // 若输入整数小于1，则右端点设为 1

    while (fabs(l-k/l) > eps)
    {
        mid = l + (r - l) /2 ;   // 防止溢出
        if (mid < k/mid)  // 防止溢出
        {
            l = mid;
        }
        else {
            r = mid;
        }
    }
    cout << l << endl;
    return 0;
}

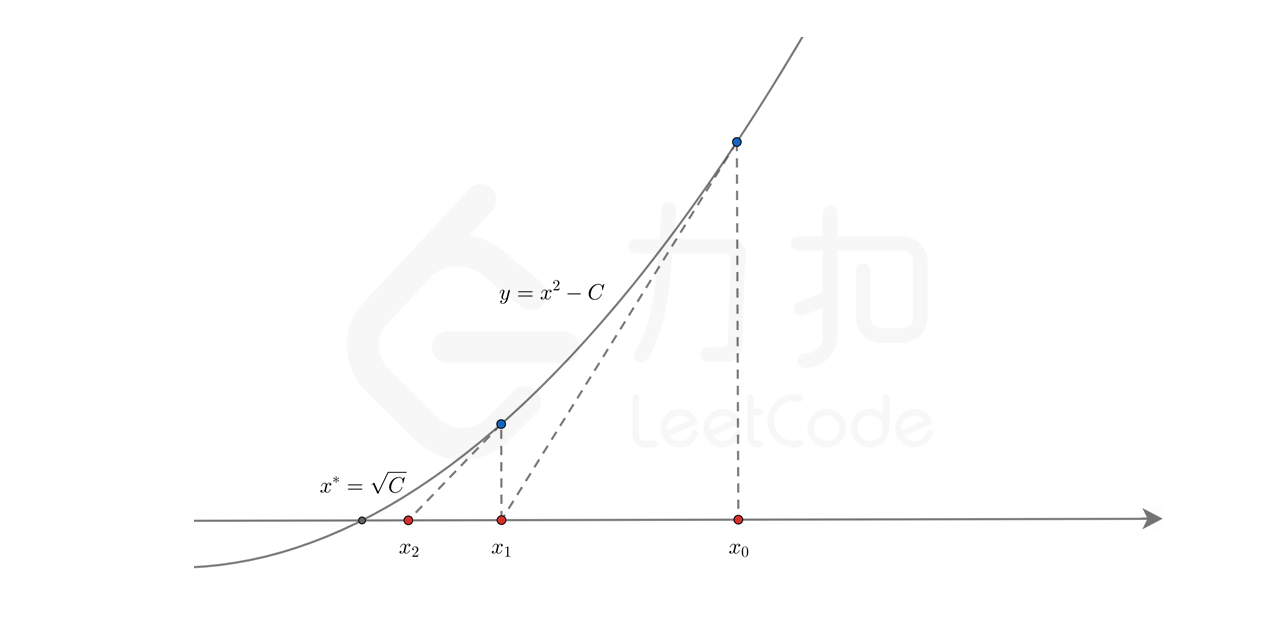
牛顿法

#include<iostream>
using namespace std;

double mysqrt(double x)
{
    if (x == 1 || x == 0)
        return x;
    double temp = x / 2;
    while (1)
    {
        double a = temp;
        temp = (temp + x / temp) / 2;
        if (fabs(a - temp) < 0.000001)
        {
            return temp;
        }
    }
}

int main()
{
    double k = 0.5;
    double result= 0.0;
    result= mysqrt(k);
    cout << result << endl;
    return 0;
}